Hamiltonian constraint of LQG
In mathematics Conflict-Driven Clause Learning (CDCL) is an efficient algorithm for solving the Boolean Satisfiability (SAT). Given a Boolean formula, the SAT problem asks for an assignment of variables so that the entire formula evaluates to true. The internal workings of CDCL SAT solvers were inspired by DPLL solvers.
Conflict Driven Clause Learning was proposed by: J. P. Marques-Silva and Karem A. Sakallah, in their paper “GRASP: A Search Algorithm for Propositional Satisfiability”. and R. J. Bayardo Jr. and R. C. Schrag, in their paper “Using CSP look-back techniques to solve real world SAT instances.”
Algorithm
To have a clear idea about the CDCL algorithm we must have background knowledge about:
- Boolean satisfiability problem SAT (Satisfiability)
- Unit clause rule (Unit propagation)
- Boolean constraint propagation (BCP).
- Resolution (logic)
- Davis–Putnam algorithm
- DPLL algorithm
Background
SAT (Satisfiability)
Satisfiability problem - Given a CNF formula, find a satisfying assignment for it.
The following formulas is in CNF:
where A,C,B are variables or literals. Both and are clauses, and denotes the negation of A.
An alternate notation for the same CNF formula is:
where A,C,B are variables or literals. Both and are clauses, and denotes the negation of A.
One satisfying assignement for this formula could be:
If we just apply brute force search to find a satisfying assignment, there are 3 variables (A,B,C) and there are 2 possible assignments (True or False) for each variable. So we have possibilities. In this small example we can use brute force to try all possible assignments and check if they satisfy our formula. But if we have million of variables and clauses then brute force search is impractical. The responsibility of a SAT solver is to find a satisfying assignment efficiently and quickly by applying different heuristics for complex CNF formulas.
Unit clause rule (unit propagation)
If an unsatisfied clause has all but one of its literals or variables evaluated at False, then the free literal must be True in order for the clause to be True. For example, if the below unsatisfied clause is evaluated with and we must have in order for the clause to be true.
Boolean constraint propagation (BCP)
The iterated application of the unit clause rule is referred to as unit propagation or Boolean constraint propagation (BCP).
Resolution
Consider two clauses and .
By applying resolution refutation we get ,
by cancelling out and .
DP Algorithm
Davis, Putnam (1960) developed this algorithm. Some properties of this algorithms are:
- Iteratively select variable for resolution till no more variable are left.
- Can discard all original clauses after each iteration.
See more details here DP Algorithm

DPLL Algorithm
Davis, Putnam, Logemann, Loveland (1962) had developed this algorithm. Some properties of this algorithms are:
- It is based on search.
- It is the basis for almost all modern SAT solvers.
- It uses learning and chronological back tracking (1996).
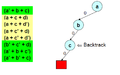
See more details here DPLL algorithm. An example with visualization of DPLL algorithm having chronological back tracking:
-
All clauses making a CNF formula
-
Pick a variable
-
Make a decision, variable a = False (0), thus green clauses becomes True
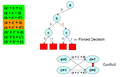
-
After several decision making, we find an implication graph that lead to a conflict.
-
Now Backtrack to immediate level and by force assign opposite value to that variable
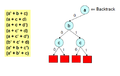
-
But force decision still lead to another conflict
-
Backtrack to previous level and make a force decision
-
Make a new decision, but it lead to a conflict
-
Make a forced decision, but again it lead to a conflict
-
Backtrack to previous level
-
Continue in this way and the final implication graph
CDCL (Conflict Driven Clause Learning)
The main difference of CDCL and DPLL is that CDCL's back jumping is non - chronological.
Conflict Driven Clause Learning works as follows.
- Select a variable and assign True or False. This is called decision state. Remember the assignment.
- Apply Boolean constraint propagation (Unit propagation).
- Build the implication graph.
- If there is any conflict then analyze the conflict and non-chronologically backtrack ("back jump") to the appropriate decision level.
- Otherwise continue from step 1 until all variable values are assigned.
Example
A visual example of CDCL algorithm:
-
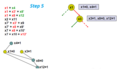
At first pick a branching variable. Yellow circles means make a decision.
-
Now apply unit propagation and it yields X4 must be True. Gray circles means force variable assignment during unit propagation. This graph is called implication graph.
-
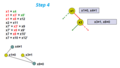
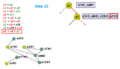
Pick another branching variable. Yellow circles means make a decision.
-
Apply unit propagation and find another new implication graph.
-
Here two variable X8 and X12 forced to be 0 and 1.
-
Pick another branching variable.
-
Find implication graph.
-
Pick another branching variable.
-
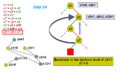
Find implication graph. Finally found a CONFLICT !!
-
Find the cut that lead to this conflict and from the cut find the conflict clause.
-
Find the clause by its negation.
-
Add the conflict clause to the rest of the clauses.
-
Non- chronological back jump to appropriate decision level.
-
Back jump and set variable values accordingly.
Pseudocode
algorithm CDCL (cnfFormula,variables):
if (UnitPropagation(cnfFormula,variables) == CONFLICT):
return UNSAT
else:
decisionLevel = 0 #Decision level
while (not AllVariablesAssigned(cnfFormula,variables)):
(variable, val) = PickBranchingVariable(cnfFormula,variables) #Decide stage
decisionLevel += 1 #Increment decision level due to new decision
insert (variable, val) in variables
if (UnitPropagation(cnfFormula,variables) == CONFLICT):
backtrackLevel = ConflictAnalysis(cnfFormula,variables)
if( backtrackLevel < 0):
return UNSAT
else:
Backtrack(cnfFormula,variables,backtrackLevel)
decisionLevel = backtrackLevel #Decrement decision level due to backtracking
return SAT
In addition to the main CDCL function, the following auxiliary functions are used:
- UnitPropagation: consists of the iterated application of the unit clause rule. If an unsatisfied clause is identified, then a conflict indication is returned.
- PickBranchingVariable: consists of selecting a variable to assign and the respective value.
- ConflictAnalysis consists of analyzing the most recent conflict and learning a new clause from the conflict.
- Backtrack: backtracks to the decision level computed by Conflict- Analysis.
- AllVariablesAssigned: tests whether all variables have been assigned, in which case the algorithm terminates indicating that the CNF formula is satisfiable. An alternative criterion to stop execution of the algorithm is to check whether all clauses are satisfied. However, in modern SAT solvers that use lazy data structures, clause state cannot be maintained accurately, and so the termination criterion must be whether all variables are assigned.
Completeness
DPLL is a sound and complete algorithm for SAT. CDCL SAT solvers implement DPLL, but can learn new clauses and backtrack non-chronologically. Clause learning with conflict analysis does not affect soundness or completeness. Conflict analysis identifies new clauses using the resolution operation. Therefore each learnt clause can be inferred from the original clauses and other learnt clauses by a sequence of resolution steps. If cN is the new learnt clause, then ϕ is satisfiable if and only if ϕ ∪ {cN} is also satisfiable. Moreover, the modified backtracking step also does not affect soundness or completeness, since backtracking information is obtained from each new learnt clause.
Applications
The main application of CDCL algorithm is in different SAT solvers including:
- MiniSAT
- Zchaff SAT
- Z3
- ManySAT etc.
The CDCL algorithm has made SAT solvers so powerful that they are being used effectively in several real world application areas like - AI planning, bioinformatics, software test pattern generation, software package dependencies, hardware and Ssoftware model checking, and cryptography.
Related algorithms
Related algorithm to CDCL are the DP and DPLL algorithm described before. DP algorithm uses resolution refutation and it has potential memory access problem. Where as DPLL algorithm is OK for randomly generated instances but bad for instances generated in practical application. We have better approach CDCL to solve such problems. Applying CDCL provides less state space search in compare to DPLL.
-
DPLL: no learning and chronological backtracking.
-
CDCL: conflict driven clause learning and non - chronological backtracking.
References
- M. Davis, H. Putnam. A Computing Procedure for Quantification Theory. J. ACM 7(3): 201-215 (1960)
- M. Davis, G. Logemann, D.W. Loveland. A machine program for theorem-proving. Commun. ACM 5(7): 394-397 (1962)
- M.W. Moskewicz, C. F. Madigan, Y. Zhao, L. Zhang, S. Malik. Chaff: Engineering an Efficient SAT Solver. DAC 2001: 530-535
- J. P. Marques-Silva and Karem A. Sakallah, “GRASP: A Search Algorithm for Propositional Satisfiability”, IEEE Trans. Computers, C-48, 5:506-521,1999.
- R. J. Bayardo Jr. and R. C. Schrag “Using CSP look-back techniques to solve real world SAT instances.” Proc. AAAI, pp. 203–208, 1997.
- L. Zhang, C. F. Madigan, M.W. Moskewicz, S. Malik. Efficient Conflict Driven Learning in Boolean Satisfiability Solver. ICCAD 2001: 279-285
- Handbook of Satisfiability Armin Biere, Marijn Heule, Hans van Maaren and Toby Walsch IOS Press, 2008.
- Presentation - "SAT-Solving: From Davis-Putnam to Zchaff and Beyond" by Lintao Zhang. (Several pictures are taken from his presentation)
Other material
Beside CDCL there are other approaches which are used to speed up SAT solvers. Some of them are -