Axis–angle representation

A problem with five linear constraints (in blue, including the non-negativity constraints). In the absence of integer constraints the feasible set is the entire region bounded by blue, but with integer constraints it is the set of red dots.

A closed feasible region of a linear programming problem with three variables is a convex polyhedron.

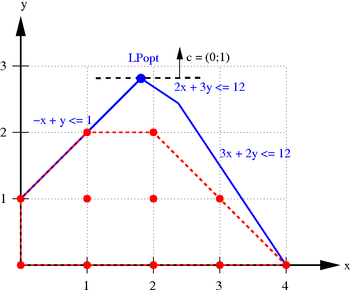
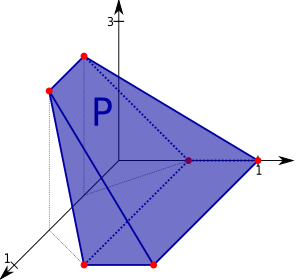
In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down.

For example, consider the problem

Minimize $x_1^2+x_2^4$

with respect to the variables $x_1$ and $x_2,$

subject to

$1\le x_1\le 10$

and

$5\le x_2\le 12.$

Here the feasible set is the set of pairs (x₁, x₂) in which the value of x₁ is at least 1 and at most 10 and the value of x₂ is at least 5 and at most 12. Note that the feasible set of the problem is separate from the objective function, which states the criterion to be optimized and which in the above example is $x_1^2+x_2^4.$

In many problems, the feasible set reflects a constraint that one or more variables must be non-negative. In pure integer programming problems, the feasible set is the set of integers (or some subset thereof). In linear programming problems, the feasible set is a convex polytope: a region in multidimensional space whose boundaries are formed by hyperplanes and whose corners are vertices.

Constraint satisfaction is the process of finding a point in the feasible region.

Convex feasible set

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.

In a linear programming problem, a series of linear constraints produces a convex feasible region of possible values for those variables. In the two-variable case this region is in the shape of a convex simple polygon.

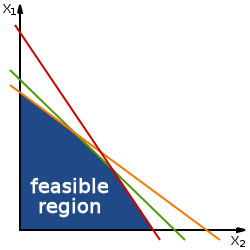
A convex feasible set is one in which a line segment connecting any two feasible points goes through only other feasible points, and not through any points outside the feasible set. Convex feasible sets arise in many types of problems, including linear programming problems, and they are of particular interest because, if the problem has a convex objective function that is to be maximized, it will generally be easier to solve in the presence of a convex feasible set and any local optimum will also be a global optimum.

No feasible set

If the constraints of an optimization problem are mutually contradictory, there are no points that satisfy all the constraints and thus the feasible region is the null set. In this case the problem has no solution and is said to be infeasible.

Bounded and unbounded feasible sets

A bounded feasible set (top) and an unbounded feasible set (bottom). The set at the bottom continues forever towards the right.

Feasible sets may be bounded or unbounded. For example, the feasible set defined by the constraint set {x ≥ 0, y ≥ 0} is unbounded because in some directions there is no limit on how far one can go and still be in the feasible region. In contrast, the feasible set formed by the constraint set {x ≥ 0, y ≥ 0, x + 2y ≤ 4} is bounded because the extent of movement in any direction is limited by the constraints.

In linear programming problems with n variables, a necessary but not sufficient condition for the feasible set to be bounded is that the number of constraints be at least n + 1 (as illustrated by the above example).

If the feasible set is unbounded, there may or may not be an optimum, depending on the specifics of the objective function. For example, if the feasible region is defined by the constraint set {x ≥ 0, y ≥ 0}, then the problem of maximizing x + y has no optimum since any candidate solution can be improved upon by increasing x or y; yet if the problem is to minimize x + y, then there is an optimum (specifically at (x, y) = (0, 0)).