Dikinase: Difference between revisions
Jump to navigation
Jump to search
en>Ulric1313 dab |
en>Pixie mNo edit summary |
||
| Line 1: | Line 1: | ||
The [[global navigation satellite system]] (GNSS) positioning for receiver's position is derived through the calculation steps, or algorithm, given below. | |||
In essence, a GNSS receiver measures the transmitting time of GNSS signals emitted from four or more GNSS satellites and these measurements are used to obtain its position (i.e., spatial coordinates) and reception time.<!-- | |||
In essence, from each received satellite signal a single measured quantity is obtained (time of arrival of information from the satellite). Four quantities need to be computed: three spatial coordinates and the absolute time. Thus, it is necessary to receive signals from a minimum of four satellites in order to solve for the four unknowns. With more than four signals available, it is possible to use the extra information to check for consistency and to improve the accuracy of the position and time. --> | |||
==Calculation steps== | |||
# A [[global navigation satellite system|global-navigation-satellite-system]] (GNSS) receiver measures the apparent transmitting time, <math>\scriptstyle \tilde{t}_i</math>, or "phase", of GNSS signals emitted from four or more GNSS [[satellite]]s (<math>\scriptstyle i \;=\; 1,\, 2,\, 3,\, 4,\, ..,\, n</math> ), simultaneously.<ref name="Misra_Enge">Misra, P. and Enge, P., Global Positioning System: Signals, Measurements, and Performance, 2nd, Ganga-Jamuna Press, 2006.</ref> | |||
# GNSS satellites broadcast the messages of satellites' [[ephemeris]], <math>\scriptstyle \boldsymbol{r}_i (t)</math>, and intrinsic clock bias (i.e., clock advance), <math>\scriptstyle\delta t_{\text{clock,sv},i} (t)</math> as the functions of ([[atomic clock|atomic]]) [[standard time]], e.g., [[GPST]].<ref name="IS-GPS">[http://www.navcen.uscg.gov/pdf/IS-GPS-200D.pdf The interface specification of NAVSTAR GLOBAL POSITIONING SYSTEM]</ref> | |||
# The transmitting time of GNSS satellite signals, <math>\scriptstyle t_i</math>, is thus derived from the non-[[closed-form expression|closed-form]] [[equations]] <math>\scriptstyle \tilde{t}_i \;=\; t_i \,+\, \delta t_{\text{clock},i} (t_i)</math> and <math>\scriptstyle \delta t_{\text{clock},i} (t_i) \;=\; \delta t_{\text{clock,sv},i} (t_i) \,+\, \delta t_{\text{orbit-relativ},\, i} (\boldsymbol{r}_i,\, \dot{\boldsymbol{r}}_i)</math>, where <math>\scriptstyle \delta t_{\text{orbit-relativ},i} (\boldsymbol{r}_i,\, \dot{\boldsymbol{r}}_i)</math> is the [[Theory of relativity|relativistic]] clock bias, periodically risen from the satellite's [[orbital eccentricity]] and Earth's [[gravity field]].<ref name="IS-GPS"/> The satellite's position and velocity are determined by <math>\scriptstyle t_i</math> as follows: <math>\scriptstyle \boldsymbol{r}_i \;=\; \boldsymbol{r}_i (t_i)</math> and <math>\scriptstyle \dot{\boldsymbol{r}}_i \;=\; \dot{\boldsymbol{r}}_i (t_i)</math>. <!-- The satellite's position is derived from <math>\scriptstyle \boldsymbol{r}_i \;=\; \boldsymbol{r}_i (t_i)</math>. --> | |||
# In the field of GNSS, "geometric range", <math>\scriptstyle r(\boldsymbol{r}_A,\, \boldsymbol{r}_B) </math>, is defined as straight range from <math>\scriptstyle\boldsymbol{r}_A</math> to <math>\scriptstyle\boldsymbol{r}_B</math> in [[inertial frame]] (e.g., [[Earth Centered Inertial]] (ECI) one), not in [[rotating frame]].<ref name="IS-GPS"/> | |||
# The receiver's position, <math>\scriptstyle \boldsymbol{r}_{\text{rec}}</math>, and reception time, <math>\scriptstyle t_{\text{rec}}</math>, satisfy the [[light-cone]] equation of <math>\scriptstyle r(\boldsymbol{r}_i,\, \boldsymbol{r}_{\text{rec}}) / c \,+\, (t_i - t_{\text{rec}}) \;=\; 0 </math> in [[inertial frame]], where <math>\scriptstyle c</math> is the [[speed of light]]. The signal [[transit time]] is <math>\scriptstyle -(t_i \,-\, t_{\text{rec}})</math>. | |||
# The above is extended to the [[Global navigation satellite system|satellite-navigation]] [[Real-time locating system|positioning]] [[equation]], <math>\scriptstyle r(\boldsymbol{r}_i,\, \boldsymbol{r}_{\text{rec}}) / c \,+\, (t_i \,-\, t_{\text{rec}}) \,+\, \delta t_{\text{atmos},i} \,-\, \delta t_{\text{meas-err},i} \;=\; 0 </math>, where <math>\scriptstyle \delta t_{\text{atmos},i}</math> is [[atmospheric delay]] (= [[ionospheric delay]] + [[tropospheric delay]]) along signal path and <math>\scriptstyle \delta t_{\text{meas-err},i}</math> is the measurement error. | |||
# The [[Gauss–Newton]] method can be used to solve the [[nonlinear]] [[least-squares problem]] for the solution: <math>\scriptstyle (\hat{\boldsymbol{r}}_{\text{rec}},\, \hat{t}_{\text{rec}}) \;=\; \arg \min \phi ( \boldsymbol{r}_{\text{rec}},\, t_{\text{rec}} )</math>, where <math>\scriptstyle \phi ( \boldsymbol{r}_{\text{rec}},\, t_{\text{rec}} ) \;=\; \sum_{i=1}^n ( \delta t_{\text{meas-err},i} / \sigma_{\delta t_{\text{meas-err},i} } )^2 </math>. Note that <math>\scriptstyle \delta t_{\text{meas-err},i}</math> should be regarded as a function of <math>\scriptstyle \boldsymbol{r}_{\text{rec}}</math> and <math>\scriptstyle t_{\text{rec}}</math>. | |||
<!-- and <math>\scriptstyle \delta t_{\text{meas-err},i} ( \boldsymbol{r}_{\text{rec}},\, t_{\text{rec}} ) \;=\; r(\boldsymbol{r}_i,\, \boldsymbol{r}_{\text{rec}}) / c \,+\, (t_i \,-\, t_{\text{rec}}) \,+\, \delta t_{\text{atmos},i} </math>. --> | |||
<!-- ( \boldsymbol{r}_{\text{rec}},\, t_{\text{rec}} ) --> | |||
<!-- , in order to obtain the solution of the receiver's position, <math>\scriptstyle \boldsymbol{r}_{\text{rec}}</math>, and reception time, <math>\scriptstyle t_{\text{rec}}</math>. --> | |||
<!-- \underset{(\boldsymbol{r}_{\text{rec}},\, t_{\text{rec}}) }{\arg \min} --> | |||
# The [[posterior distribution]] of <math>\scriptstyle \boldsymbol{r}_{\text{rec}}</math> and <math>\scriptstyle t_{\text{rec}}</math> is proportional to <math>\scriptstyle \exp ( -\frac{1}{2} \phi ( \boldsymbol{r}_{\text{rec}},\, t_{\text{rec}} ) )</math>, whose [[Mode (statistics)|mode]] is <math>\scriptstyle (\hat{\boldsymbol{r}}_{\text{rec}},\, \hat{t}_{\text{rec}})</math>. Their inference is formalized as [[maximum a posteriori estimation]]. | |||
# The [[posterior distribution]] of <math>\scriptstyle \boldsymbol{r}_{\text{rec}}</math> is proportional to <math>\scriptstyle \int_{-\infty}^\infty \exp ( -\frac{1}{2} \phi ( \boldsymbol{r}_{\text{rec}},\, t_{\text{rec}} ) ) \, d t_{\text{rec}}</math>. | |||
==The solution illustrated == | |||
<gallery> | |||
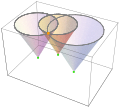
Image:Light cones.svg|alt=|Essentially, the solution, <math>\scriptstyle (\hat{\boldsymbol{r}}_{\text{rec}},\, \hat{t}_{\text{rec}})</math>, is the intersection of [[light cone]]s. | |||
Image:Evolution light cones 0.gif|alt=|The [[posterior distribution]] of the solution is derived from the product of the distribution of propagating spherical surfaces. (See [http://commons.wikimedia.org/wiki/File:Evolution_light_cones.gif animation].) | |||
</gallery><!-- | |||
=== Animation === | |||
[[:File:Evolution light cones.gif|The posterior distribution of the solution is derived from the product of the distribution of propagating spherical surfaces.]] | |||
--> | |||
==The GPS case == | |||
* For [[Global Positioning System]] (GPS),<ref name="IS-GPS"/> the non-closed-form equations in step 3 result in | |||
<!-- <math>\scriptstyle \Delta t_i (t_i,\, E_i) \;\equiv\; t_i \,+\, \delta t_{\text{clock},i} (t_i,\, E_i) \,-\, \tilde{t}_i \;=\; 0</math> and <math>\scriptstyle \Delta M_i (t_i,\, E_i) \;\equiv\; M_i (t_i) \,-\, (E_i \,-\, e_i \sin E_i) \;=\; 0</math>, --> | |||
:<math> \scriptstyle \begin{cases} | |||
\scriptstyle \Delta t_i (t_i,\, E_i) \;\triangleq\; t_i \,+\, \delta t_{\text{clock},i} (t_i,\, E_i) \,-\, \tilde{t}_i \;=\; 0, \\ | |||
\scriptstyle \Delta M_i (t_i,\, E_i) \;\triangleq\; M_i (t_i) \,-\, (E_i \,-\, e_i \sin E_i) \;=\; 0, | |||
\end{cases} </math> | |||
in which <math>\scriptstyle E_i</math> is the orbital [[eccentric anomaly]] of satellite <math>i</math>, <math>\scriptstyle M_i</math> is the [[mean anomaly]], <math>\scriptstyle e_i</math> is the [[orbital eccentricity|eccentricity]], and <math>\scriptstyle \delta t_{\text{clock},i} (t_i,\, E_i) \;=\; \delta t_{\text{clock,sv},i} (t_i) \,+\, \delta t_{\text{orbit-relativ},i} (E_i)</math>. | |||
* The above can be solved by using the [[bivariate analysis|bivariate]] [[Newton-Raphson]] method on <math>\scriptstyle t_i</math> and <math>\scriptstyle E_i</math>. Two times of iteration will be necessary and sufficient in most cases. Its iterative update will be described by using the approximated [[inverse (mathematics)|inverse]] of [[Jacobian]] matrix as follows: | |||
<math>\scriptscriptstyle | |||
\begin{pmatrix} | |||
t_i \\ | |||
E_i \\ | |||
\end{pmatrix} | |||
\leftarrow | |||
\begin{pmatrix} | |||
t_i \\ | |||
E_i \\ | |||
\end{pmatrix} | |||
- | |||
\begin{pmatrix} | |||
1 && 0 \\ | |||
\frac{\dot{M}_i (t_i)}{1 - e_i \cos E_i} && -\frac{1}{1 - e_i \cos E_i} \\ | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\Delta t_i \\ | |||
\Delta M_i \\ | |||
\end{pmatrix} | |||
</math> | |||
* [[Tropospheric delay]] should not be ignored, while the [[Global Positioning System]] (GPS) specification <ref name="IS-GPS"/> doesn't provide its detailed description. <!--mention it clearly.--> | |||
==The GLONASS case == | |||
* The [[GLONASS]] ephemerides don't provide clock biases <math>\scriptstyle\delta t_{\text{clock,sv},i} (t)</math>, but <math>\scriptstyle\delta t_{\text{clock},i} (t)</math>. | |||
==Note== | |||
* In the field of GNSS, <math>\scriptstyle \tilde{r}_i \;=\; -c (\tilde{t}_i \,-\, \tilde{t}_{\text{rec}})</math> is called [[pseudorange]], where <math>\scriptstyle \tilde{t}_{\text{rec}}</math> is a provisional reception time of the receiver. <math>\scriptstyle \delta t_{\text{clock,rec}} \;=\; \tilde{t}_{\text{rec}} \,-\, t_{\text{rec}}</math> is called receiver's clock bias (i.e., clock advance).<ref name="Misra_Enge"/> | |||
* Standard GNSS receivers output <math>\scriptstyle \tilde{r}_i</math> and <math>\scriptstyle \tilde{t}_{\text{rec}}</math> per an observation [[Epoch (astronomy)|epoch]]. | |||
* The temporal variation in the relativistic clock bias of satellite is linear if its orbit is circular (and thus its velocity is uniform in inertial frame). | |||
* The signal [[transit time]] is expressed as <math>\scriptstyle -(t_i - t_{\text{rec}}) \;=\; \tilde{r}_i/c \,+\, \delta t_{\text{clock},i} \,-\, \delta t_{\text{clock,rec}}</math>, whose right side is [[round-off error|round-off-error]] resistive during calculation. | |||
* The geometric range is calculated as <math>\scriptstyle r(\boldsymbol{r}_i,\, \boldsymbol{r}_{\text{rec}}) \;=\; | \Omega_{\text{E}} (t_i \,-\, t_{\text{rec}}) \boldsymbol{r}_{i,\text{ECEF}} \,-\, \boldsymbol{r}_{\text{rec,ECEF}} |</math>, where the [[ECEF|Earth-centred Earth-fixed]] (ECEF) rotating frame (e.g., [[WGS84]] or [[International Terrestrial Reference Frame|ITRF]]) is used in the right side and <math>\scriptstyle \Omega_{\text{E}}</math> is the Earth rotating matrix with the argument of the signal [[transit time]].<ref name="IS-GPS"/> The matrix can be factorized as <math>\scriptstyle \Omega_{\text{E}} (t_i \,-\, t_{\text{rec}}) \;=\; \Omega_{\text{E}} (\delta t_{\text{clock,rec}}) \Omega_{\text{E}} (-\tilde{r}_i/c \,-\, \delta t_{\text{clock},i}) </math>. | |||
* The line-of-sight unit vector of satellite observed at <math>\scriptstyle \boldsymbol{r}_{\text{rec,ECEF}}</math> is described as: <math>\scriptstyle \boldsymbol{e}_{i, \text{rec,ECEF}} \;=\; -\frac{\partial r(\boldsymbol{r}_i,\, \boldsymbol{r}_{\text{rec}})}{\partial \boldsymbol{r}_{\text{rec,ECEF}}} </math>. | |||
* The [[Global navigation satellite system|satellite-navigation]] [[Real-time locating system|positioning]] [[equation]] may be expressed by using the [[variable (mathematics)|variables]] <math>\scriptstyle \boldsymbol{r}_{\text{rec,ECEF}}</math> and <math>\scriptstyle \delta t_{\text{clock,rec}}</math>. | |||
* The [[nonlinearity]] of the vertical dependency of [[tropospheric delay]] degrades the convergence efficiency in the [[Gauss–Newton]] iterations in step 7. | |||
* The above notation is different from that in the Wikipedia articles, 'Position calculation introduction' and 'Position calculation advanced', of [[Global Positioning System]] (GPS). | |||
==References== | |||
<references/> | |||
{{DEFAULTSORT:Gnss Positioning Calculation}} | |||
[[Category:Satellite navigation systems]] | |||
Latest revision as of 15:31, 28 January 2014
The global navigation satellite system (GNSS) positioning for receiver's position is derived through the calculation steps, or algorithm, given below. In essence, a GNSS receiver measures the transmitting time of GNSS signals emitted from four or more GNSS satellites and these measurements are used to obtain its position (i.e., spatial coordinates) and reception time.
Calculation steps
- A global-navigation-satellite-system (GNSS) receiver measures the apparent transmitting time, , or "phase", of GNSS signals emitted from four or more GNSS satellites ( ), simultaneously.[1]
- GNSS satellites broadcast the messages of satellites' ephemeris, , and intrinsic clock bias (i.e., clock advance), as the functions of (atomic) standard time, e.g., GPST.[2]
- The transmitting time of GNSS satellite signals, , is thus derived from the non-closed-form equations and , where is the relativistic clock bias, periodically risen from the satellite's orbital eccentricity and Earth's gravity field.[2] The satellite's position and velocity are determined by as follows: and .
- In the field of GNSS, "geometric range", , is defined as straight range from to in inertial frame (e.g., Earth Centered Inertial (ECI) one), not in rotating frame.[2]
- The receiver's position, , and reception time, , satisfy the light-cone equation of in inertial frame, where is the speed of light. The signal transit time is .
- The above is extended to the satellite-navigation positioning equation, , where is atmospheric delay (= ionospheric delay + tropospheric delay) along signal path and is the measurement error.
- The Gauss–Newton method can be used to solve the nonlinear least-squares problem for the solution: , where . Note that should be regarded as a function of and .
- The posterior distribution of and is proportional to , whose mode is . Their inference is formalized as maximum a posteriori estimation.
- The posterior distribution of is proportional to .
The solution illustrated
-
Essentially, the solution, , is the intersection of light cones.
-
The posterior distribution of the solution is derived from the product of the distribution of propagating spherical surfaces. (See animation.)
The GPS case
- For Global Positioning System (GPS),[2] the non-closed-form equations in step 3 result in
in which is the orbital eccentric anomaly of satellite , is the mean anomaly, is the eccentricity, and .
- The above can be solved by using the bivariate Newton-Raphson method on and . Two times of iteration will be necessary and sufficient in most cases. Its iterative update will be described by using the approximated inverse of Jacobian matrix as follows:
- Tropospheric delay should not be ignored, while the Global Positioning System (GPS) specification [2] doesn't provide its detailed description.
The GLONASS case
- The GLONASS ephemerides don't provide clock biases , but .
Note
- In the field of GNSS, is called pseudorange, where is a provisional reception time of the receiver. is called receiver's clock bias (i.e., clock advance).[1]
- Standard GNSS receivers output and per an observation epoch.
- The temporal variation in the relativistic clock bias of satellite is linear if its orbit is circular (and thus its velocity is uniform in inertial frame).
- The signal transit time is expressed as , whose right side is round-off-error resistive during calculation.
- The geometric range is calculated as , where the Earth-centred Earth-fixed (ECEF) rotating frame (e.g., WGS84 or ITRF) is used in the right side and is the Earth rotating matrix with the argument of the signal transit time.[2] The matrix can be factorized as .
- The line-of-sight unit vector of satellite observed at is described as: .
- The satellite-navigation positioning equation may be expressed by using the variables and .
- The nonlinearity of the vertical dependency of tropospheric delay degrades the convergence efficiency in the Gauss–Newton iterations in step 7.
- The above notation is different from that in the Wikipedia articles, 'Position calculation introduction' and 'Position calculation advanced', of Global Positioning System (GPS).