Aspherical space: Difference between revisions
en>SchreiberBike Disambiguation needed for the link Lattice (mathematics) |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Slice sampling''' is a type of [[Markov chain Monte Carlo]] [[algorithm]] for [[pseudo-random number sampling]], i.e. for drawing random samples from a statistical distribution. The method is based on the observation that to sample a [[random variable]] one can sample uniformly from the region under the graph of its density function.<ref>Damlen, P., Wakefield, J., & Walker, S. (1999). Gibbs sampling for Bayesian non‐conjugate and hierarchical models by using auxiliary variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 61(2), 331-344.Chicago</ref><ref name="radford03">{{cite journal | |||
|first=Radford M. |last=Neal | |||
|title=Slice Sampling | |||
|journal=[[Annals of Statistics]] | |||
|volume=31 |issue=3 |pages=705–767 |year=2003 | |||
|doi=10.1214/aos/1056562461 | |||
|mr=1994729 | zbl = 1051.65007 | |||
}}</ref><ref name="bishop06">{{cite book | |||
| last = Bishop | |||
| first = Christopher | |||
| title = Pattern Recognition and Machine Learning | |||
| publisher = [[Springer Science+Business Media|Springer]] | |||
| year = 2006 | |||
| chapter = 11.4: Slice sampling | |||
| isbn = 0387310738 | |||
}}</ref> | |||
To visualize this motivation, imagine printing out a simple bell curve and throwing darts at it. Assume that the darts are uniformly distributed around the board. Now take off all of the darts that are outside the curve (i.e. perform [[rejection sampling]]). The x-positions of the remaining darts will be distributed according to the bell curve. This is because there is the most room for the darts to land where curve is highest and thus the probability density is greatest. | |||
Slice sampling, in its simplest form, samples uniformly from underneath the curve f(x) without the need to reject any points, as follows: | |||
#Choose a starting value x<sub>0</sub> for which f(x<sub>0</sub>)>0. | |||
#Sample a y value uniformly between 0 and f(x<sub>0</sub>). | |||
#Draw a horizontal line across the curve at this y position. | |||
#Sample a point (x,y) from the line segments within the curve. | |||
#Repeat from step 2 using the new x value. | |||
The motivation here is that one way to sample a point uniformly from within an arbitrary curve is first to draw thin uniform-height horizontal slices across the whole curve. Then, we can sample a point within the curve by randomly selecting a slice that falls at or below the curve at the x-position from the previous iteration, then randomly picking an x-position somewhere along the slice. By using the x-position from the previous iteration of the algorithm, in the long run we select slices with probabilities proportional to the lengths of their segments within the curve. | |||
Generally, the trickiest part of this algorithm is finding the bounds of the horizontal slice, which involves inverting the function describing the distribution being sampled from. This is especially problematic for multi-modal distributions, where the slice may consist of multiple discontiguous parts. It is often possible to use a form of rejection sampling to overcome this, where we sample from a larger slice that is known to include the desired slice in question, and then discard points outside of the desired slice. | |||
Note also that this algorithm can be used to sample from the area under ''any'' curve, regardless of whether the function integrates to 1. In fact, scaling a function by a constant has no effect on the sampled x-positions. This means that the algorithm can be used to sample from a distribution whose [[probability density function]] is only known up to a constant (i.e. whose [[normalizing constant]] is unknown), which is common in [[computational statistics]]. | |||
==Implementation== | |||
Slice sampling gets its name from the first step: defining a ''slice'' by sampling from an auxiliary variable <math>Y</math>. This variable is sampled from <math>[0, f(x)]</math>, where <math>f(x)</math> is either the probability density function (pdf) of ''X'' or is at least proportional to its pdf. This defines a slice of ''X'' where <math>f(x) > Y</math>. In other words, we are now looking at a region of ''X'' where the probability density is at least <math>Y</math>. Then the next value of ''X'' is sampled uniformly from this slice. A new value of <math>Y</math> is sampled, then ''X'', and so on. This can be visualized as alternatively sampling the y-position and then the x-position of points under pdf, thus the ''X''s are from the desired distribution. The <math>Y</math> values have no particular consequences or interpretations outside of their usefulness for the procedure. | |||
If both the pdf and its inverse are available, and the distribution is unimodal, then finding the slice and sampling from it are simple. If not, a stepping-out procedure can be used to find a region whose endpoints fall outside the slice. Then, a sample can be drawn from the slice using [[rejection sampling]]. Various procedures for this are described in detail by Neal.<ref name="radford03"/> | |||
Note that, in contrast to many available methods for generating random numbers from non-uniform distributions, random variates generated directly by this approach will exhibit serial statistical dependence. This is because to draw the next sample, we define the slice based on the value of f(x) for the current sample. | |||
==Motivation== | |||
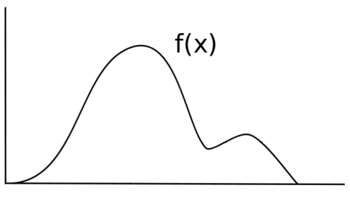
Suppose you want to sample some random variable ''X'' with distribution f(x). Suppose that the following is the graph of f(x). The height of f(x) corresponds to the likelihood at that point. | |||
[[File:Some probability distribution.png|350px|alt=alt text|]] | |||
If you were to uniformly sample ''X'', each value would have the same likelihood of being sampled, and your distribution would be of the form f(x)=y for some ''y'' value instead of some non-uniform function f(x). Instead of the original black line, your new distribution would look more like the blue line. | |||
[[File:A horizontally sliced distribution.png|350px|alt=alt text|]] | |||
In order to sample ''X'' in a manner which will retain the distribution f(x), some sampling technique must be used which takes into account the varied likelihoods for each range of f(x). | |||
==Compared to Other Methods== | |||
Slice sampling is a Markov chain method and as such serves the same purpose as Gibbs sampling and Metropolis. Unlike Metropolis, there is no need to manually tune the candidate function or candidate standard deviation. | |||
Recall that Metropolis is sensitive to step size. If the step size is too small random walk causes slow decorrelation. If the step size is too large there is great inefficiency due to a high rejection rate. | |||
In contrast to Metropolis, slice sampling automatically adjusts the step size to match the local shape of the density function. Implementation is arguably easier and more efficient than Gibbs sampling or simple Metropolis updates. | |||
Note that, in contrast to many available methods for generating random numbers from non-uniform distributions, random variates generated directly by this approach will exhibit serial statistical dependence. In other words, not all points have the same independent likelihood of selection. | |||
Slice Sampling requires that the distribution to be sampled be evaluable. One way to relax this requirement is to substitute an evaluable distribution which is proportional to the true unevaluable distribution. | |||
==Univariate Case== | |||
[[File:A horizontally and vertically sliced distribution.png|thumb|350px|alt=alt text|For a given sample x, a value for y is chosen from [0, f(x)], which defines a "slice" of the distribution (shown by the solid horizontal line). In this case, there are two slices separated by an area outside the range of the distribution.]] | |||
To sample a random variable ''X'' with density f(x) we introduce an auxiliary variable ''Y'' and iterate as follows: | |||
*Given a sample ''x'' we choose ''y'' uniformly at random from the interval [0, f(x)]; | |||
*given ''y'' we choose ''x'' uniformly at random from the set <math>f^{-1}[y, +\infty)</math>. | |||
*The sample of ''x'' is obtained by ignoring the ''y'' values. | |||
Our auxiliary variable ''Y'' represents a horizontal "slice" of the distribution. The rest of each iteration is dedicated to sampling an ''x'' value from the slice which is representative of the density of the region being considered. | |||
In practice, sampling from a horizontal slice of a multimodal distribution is difficult. There is a tension between obtaining a large sampling region and thereby making possible large moves in the distribution space, and obtaining a simpler sampling region to increase efficiency. One option for simplifying this process is regional expansion and contraction. | |||
*First, a width parameter ''w'' is used to define the area containing the given ''x'' value. Each endpoint of this area is tested to see if it lies outside the given slice. If not, the region is extended in the appropriate direction(s) by ''w'' until the end both endpoints lie outside the slice. | |||
*A candidate sample is selected uniformly from within this region. If the candidate sample lies inside of the slice, then it is accepted as the new sample. If it lies outside of the slice, the candidate point becomes the new boundary for the region. A new candidate sample is taken uniformly. The process repeats until the candidate sample is within the slice. (See diagram for a visual example). | |||
[[Image:summary of slice sampling.png|thumb|center|500px|alt=alt text|Finding a sample given a set of slices (the slices are represented here as blue lines and correspond to the solid line slices in the previous graph of f(x) ). a) A width parameter ''w'' is set. b) A region of width ''w'' is identified around a given point <math>x_0</math>. c) The region is expanded by ''w'' until both endpoints are outside of the considered slice. d) <math>x_1</math> is selected uniformly from the region. e) Since <math>x_1</math> lies outside the considered slice, the region's left bound is adjusted to <math>x_1</math>. f) Another uniform sample <math>x</math> is taken and accepted as the sample since it lies within the considered slice.]] | |||
==Multivariate Methods== | |||
===Treating each variable independently=== | |||
Single variable slice sampling can be used in the multivariate case by sampling each variable in turn repeatedly, as in Gibbs sampling. To do so requires that we can compute, for each component <math>x_i</math> a function that is proportional to <math>p(x_i|x_0...x_n)</math>. | |||
To prevent random walk behavior, overrelaxation methods can be used to update each variable in turn. Overrelaxation chooses a new value on the opposite side of the mode from the current value, as opposed to choosing a new independent value from the distribution as done in Gibbs. | |||
===Hyperrectangle slice sampling=== | |||
This method adapts the univariate algorithm to the multivariate case by substituting a hyperrectangle for the one-dimensional ''w'' region used in the original. The hyperrectangle ''H'' is initialized to a random position over the slice. ''H'' is then shrunken as points from it are rejected. | |||
===Reflective slice sampling=== | |||
Reflective slice sampling is a technique to suppress random walk behavior in which the successive candidate samples of distribution f(x) are kept within the bounds of the slice by "reflecting" the direction of sampling inward toward the slice once the boundary has been hit. | |||
In this graphical representation of reflective sampling, the shape indicates the bounds of a sampling slice. The dots indicate start and stopping points of a sampling walk. When the samples hit the bounds of the slice, the direction of sampling is "reflected" back into the slice. | |||
[[File:An example of reflection sampling.png|350px|alt=alt text]] | |||
==Example== | |||
Let us consider a single variable example. Suppose our true distribution <math>g(x)\sim N(0,5)</math>. So: | |||
<math>f(x) = \frac{1}{\sqrt{2\pi*5^2}} * e^{ -\frac{(x-0)^2}{2*5^2} }</math> | |||
*We first draw a uniform random value ''y'' from the range of f(x) in order to define our slice(es). Suppose y=0.01. | |||
*Next, we set our width parameter ''w'' which we will use to expand our region of consideration. Suppose w=2. | |||
*Next, we need an initial value for ''x''. We draw ''x'' from the uniform distribution within the domain of f(x) at our current ''y''. Suppose x=2. | |||
*Because x=2 and w=2, our current region of interest is bounded by (1,3). | |||
*Now, each endpoint of this area is tested to see if it lies outside the given slice. Our right bound lies outside our slice, but the left value does not. We expand the left bound by adding ''w'' to it until it extends past the limit of the slice. After this process, the new bounds of our region of interest are (-4,3). | |||
*Next, we take a uniform sample within (-4,3). Suppose this sample yields x=-3.9. Though this sample is within our region of interest, it does not lie within our slice, so we modify the left bound of our region of interest to this point. Now we take a uniform sample from (-3.9,3). This time our sample yields x=1, which is within our slice, and thus is our accepted sample. Had our new ''x'' not been within our slice, we would continue the shrinking/resampling process until a valid ''x'' within bounds is found. | |||
==Another Example== | |||
To sample from the [[normal distribution]] <math>N(0,1)</math> we first choose an initial ''x'' -- say 0. After each sample of ''x'' we choose ''y'' uniformly at random from <math>(0, e^{-x^2/2}/\sqrt{2\pi}]</math>, which is bounded the pdf of <math>N(0,1)</math>. After each ''y'' sample we choose ''x'' uniformly at random from <math>[-\alpha, \alpha]</math> where <math>\alpha = \sqrt{-2\ln(y\sqrt{2\pi})}</math>. This is the slice where <math>f(x) > y</math>. | |||
An implementation in the [[Macsyma]] language is: | |||
<source lang="smalltalk"> | |||
slice(x):=block([y,alpha], | |||
y:random( exp(-x^2/2.0)/sqrt(2.0*dfloat(%pi))), | |||
alpha:sqrt(-2.0*ln(y*sqrt(2.0*dfloat(%pi)))), | |||
x:signum(random())*random(alpha) | |||
); | |||
</source> | |||
==See also== | |||
* [[Markov chain Monte Carlo]] | |||
==References== | |||
<references/> | |||
==External links== | |||
* http://www.probability.ca/jeff/java/slice.html | |||
[[Category:Markov chain Monte Carlo]] | |||
[[Category:Non-uniform random numbers]] | |||
Revision as of 20:34, 16 June 2013
Slice sampling is a type of Markov chain Monte Carlo algorithm for pseudo-random number sampling, i.e. for drawing random samples from a statistical distribution. The method is based on the observation that to sample a random variable one can sample uniformly from the region under the graph of its density function.[1][2][3]
To visualize this motivation, imagine printing out a simple bell curve and throwing darts at it. Assume that the darts are uniformly distributed around the board. Now take off all of the darts that are outside the curve (i.e. perform rejection sampling). The x-positions of the remaining darts will be distributed according to the bell curve. This is because there is the most room for the darts to land where curve is highest and thus the probability density is greatest.
Slice sampling, in its simplest form, samples uniformly from underneath the curve f(x) without the need to reject any points, as follows:
- Choose a starting value x0 for which f(x0)>0.
- Sample a y value uniformly between 0 and f(x0).
- Draw a horizontal line across the curve at this y position.
- Sample a point (x,y) from the line segments within the curve.
- Repeat from step 2 using the new x value.
The motivation here is that one way to sample a point uniformly from within an arbitrary curve is first to draw thin uniform-height horizontal slices across the whole curve. Then, we can sample a point within the curve by randomly selecting a slice that falls at or below the curve at the x-position from the previous iteration, then randomly picking an x-position somewhere along the slice. By using the x-position from the previous iteration of the algorithm, in the long run we select slices with probabilities proportional to the lengths of their segments within the curve.
Generally, the trickiest part of this algorithm is finding the bounds of the horizontal slice, which involves inverting the function describing the distribution being sampled from. This is especially problematic for multi-modal distributions, where the slice may consist of multiple discontiguous parts. It is often possible to use a form of rejection sampling to overcome this, where we sample from a larger slice that is known to include the desired slice in question, and then discard points outside of the desired slice.
Note also that this algorithm can be used to sample from the area under any curve, regardless of whether the function integrates to 1. In fact, scaling a function by a constant has no effect on the sampled x-positions. This means that the algorithm can be used to sample from a distribution whose probability density function is only known up to a constant (i.e. whose normalizing constant is unknown), which is common in computational statistics.
Implementation
Slice sampling gets its name from the first step: defining a slice by sampling from an auxiliary variable . This variable is sampled from , where is either the probability density function (pdf) of X or is at least proportional to its pdf. This defines a slice of X where . In other words, we are now looking at a region of X where the probability density is at least . Then the next value of X is sampled uniformly from this slice. A new value of is sampled, then X, and so on. This can be visualized as alternatively sampling the y-position and then the x-position of points under pdf, thus the Xs are from the desired distribution. The values have no particular consequences or interpretations outside of their usefulness for the procedure.
If both the pdf and its inverse are available, and the distribution is unimodal, then finding the slice and sampling from it are simple. If not, a stepping-out procedure can be used to find a region whose endpoints fall outside the slice. Then, a sample can be drawn from the slice using rejection sampling. Various procedures for this are described in detail by Neal.[2]
Note that, in contrast to many available methods for generating random numbers from non-uniform distributions, random variates generated directly by this approach will exhibit serial statistical dependence. This is because to draw the next sample, we define the slice based on the value of f(x) for the current sample.
Motivation
Suppose you want to sample some random variable X with distribution f(x). Suppose that the following is the graph of f(x). The height of f(x) corresponds to the likelihood at that point.
If you were to uniformly sample X, each value would have the same likelihood of being sampled, and your distribution would be of the form f(x)=y for some y value instead of some non-uniform function f(x). Instead of the original black line, your new distribution would look more like the blue line.
In order to sample X in a manner which will retain the distribution f(x), some sampling technique must be used which takes into account the varied likelihoods for each range of f(x).
Compared to Other Methods
Slice sampling is a Markov chain method and as such serves the same purpose as Gibbs sampling and Metropolis. Unlike Metropolis, there is no need to manually tune the candidate function or candidate standard deviation.
Recall that Metropolis is sensitive to step size. If the step size is too small random walk causes slow decorrelation. If the step size is too large there is great inefficiency due to a high rejection rate.
In contrast to Metropolis, slice sampling automatically adjusts the step size to match the local shape of the density function. Implementation is arguably easier and more efficient than Gibbs sampling or simple Metropolis updates.
Note that, in contrast to many available methods for generating random numbers from non-uniform distributions, random variates generated directly by this approach will exhibit serial statistical dependence. In other words, not all points have the same independent likelihood of selection.
Slice Sampling requires that the distribution to be sampled be evaluable. One way to relax this requirement is to substitute an evaluable distribution which is proportional to the true unevaluable distribution.
Univariate Case

To sample a random variable X with density f(x) we introduce an auxiliary variable Y and iterate as follows:
- Given a sample x we choose y uniformly at random from the interval [0, f(x)];
- given y we choose x uniformly at random from the set .
- The sample of x is obtained by ignoring the y values.
Our auxiliary variable Y represents a horizontal "slice" of the distribution. The rest of each iteration is dedicated to sampling an x value from the slice which is representative of the density of the region being considered.
In practice, sampling from a horizontal slice of a multimodal distribution is difficult. There is a tension between obtaining a large sampling region and thereby making possible large moves in the distribution space, and obtaining a simpler sampling region to increase efficiency. One option for simplifying this process is regional expansion and contraction.
- First, a width parameter w is used to define the area containing the given x value. Each endpoint of this area is tested to see if it lies outside the given slice. If not, the region is extended in the appropriate direction(s) by w until the end both endpoints lie outside the slice.
- A candidate sample is selected uniformly from within this region. If the candidate sample lies inside of the slice, then it is accepted as the new sample. If it lies outside of the slice, the candidate point becomes the new boundary for the region. A new candidate sample is taken uniformly. The process repeats until the candidate sample is within the slice. (See diagram for a visual example).

Multivariate Methods
Treating each variable independently
Single variable slice sampling can be used in the multivariate case by sampling each variable in turn repeatedly, as in Gibbs sampling. To do so requires that we can compute, for each component a function that is proportional to .
To prevent random walk behavior, overrelaxation methods can be used to update each variable in turn. Overrelaxation chooses a new value on the opposite side of the mode from the current value, as opposed to choosing a new independent value from the distribution as done in Gibbs.
Hyperrectangle slice sampling
This method adapts the univariate algorithm to the multivariate case by substituting a hyperrectangle for the one-dimensional w region used in the original. The hyperrectangle H is initialized to a random position over the slice. H is then shrunken as points from it are rejected.
Reflective slice sampling
Reflective slice sampling is a technique to suppress random walk behavior in which the successive candidate samples of distribution f(x) are kept within the bounds of the slice by "reflecting" the direction of sampling inward toward the slice once the boundary has been hit.
In this graphical representation of reflective sampling, the shape indicates the bounds of a sampling slice. The dots indicate start and stopping points of a sampling walk. When the samples hit the bounds of the slice, the direction of sampling is "reflected" back into the slice.
Example
Let us consider a single variable example. Suppose our true distribution . So:
- We first draw a uniform random value y from the range of f(x) in order to define our slice(es). Suppose y=0.01.
- Next, we set our width parameter w which we will use to expand our region of consideration. Suppose w=2.
- Next, we need an initial value for x. We draw x from the uniform distribution within the domain of f(x) at our current y. Suppose x=2.
- Because x=2 and w=2, our current region of interest is bounded by (1,3).
- Now, each endpoint of this area is tested to see if it lies outside the given slice. Our right bound lies outside our slice, but the left value does not. We expand the left bound by adding w to it until it extends past the limit of the slice. After this process, the new bounds of our region of interest are (-4,3).
- Next, we take a uniform sample within (-4,3). Suppose this sample yields x=-3.9. Though this sample is within our region of interest, it does not lie within our slice, so we modify the left bound of our region of interest to this point. Now we take a uniform sample from (-3.9,3). This time our sample yields x=1, which is within our slice, and thus is our accepted sample. Had our new x not been within our slice, we would continue the shrinking/resampling process until a valid x within bounds is found.
Another Example
To sample from the normal distribution we first choose an initial x -- say 0. After each sample of x we choose y uniformly at random from , which is bounded the pdf of . After each y sample we choose x uniformly at random from where . This is the slice where .
An implementation in the Macsyma language is:
slice(x):=block([y,alpha],
y:random( exp(-x^2/2.0)/sqrt(2.0*dfloat(%pi))),
alpha:sqrt(-2.0*ln(y*sqrt(2.0*dfloat(%pi)))),
x:signum(random())*random(alpha)
);
See also
References
- ↑ Damlen, P., Wakefield, J., & Walker, S. (1999). Gibbs sampling for Bayesian non‐conjugate and hierarchical models by using auxiliary variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 61(2), 331-344.Chicago
- ↑ 2.0 2.1 One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

![{\displaystyle [0,f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aab098c7371ce16e69a2e14b79228f7dc47e547)













![{\displaystyle (0,e^{-x^{2}/2}/{\sqrt {2\pi }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/781bcb189d0d28e28cbaa780f87e24924df23b51)
![{\displaystyle [-\alpha ,\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6aaee8f359da96b8f4b1c02a27cbdadf9adf313)

