Space tether: Difference between revisions
en>Nnemo |
en>Monkbot |
||
| Line 1: | Line 1: | ||
[[File:Kapitza pendulum.svg|thumb|Drawing showing how a Kapitza pendulum can be constructed: a motor rotates a crank at a high speed, the crank vibrates a lever arm up and down which the pendulum is attached to with a pivot.]] | |||
'''Kapitza's pendulum''' is a rigid [[pendulum]] in which the pivot point vibrates in a vertical direction, up and down. It is named after Russian [[Nobel prize|Nobel laureate]] physicist [[Pyotr Kapitza]], who in 1951 developed a theory which successfully explains some of its unusual properties.<ref name="Kapitza">P.L. Kapitza, “Dynamic stability of a pendulum when its point of suspension vibrates”, Soviet Phys. JETP 21, 588–592 (1951); P.L. Kapitza, “Pendulum with a vibrating suspension” Usp. Fiz. Nauk, 44, 7-15 (1951).</ref> The unique feature of the Kapitza pendulum is that the vibrating suspension can cause it to balance stably in an inverted position, with the bob above the suspension point. In the usual [[Pendulum (mathematics)|pendulum]] with a fixed suspension, the only stable equilibrium position is with the bob hanging below the suspension point; the inverted position is a point of [[Mechanical equilibrium|unstable equilibrium]], and the smallest perturbation moves the pendulum out of equilibrium. In [[nonlinear control theory]] the Kapitza pendulum is used as an example of a [[parametric oscillator]] that demonstrates the concept of "dynamic stabilization". | |||
The pendulum was first described by A. Stephenson in 1908, who found that the upper vertical position of the pendulum might be stable when the driving frequency is fast<ref>A. Stephenson "On an induced stability" Phil. Mag. 15, 233 (1908). [http://www.tandfonline.com/doi/abs/10.1080/14786440809463763]</ref> Yet until the 1950s there was no explanation for this highly unusual and counterintuitive phenomenon. Pyotr Kapitza was the first to analyze it in 1951.<ref name="Kapitza" /> He carried out a number of experimental studies and as well provided an analytical insight into the reasons of stability by splitting the motion into "fast" and "slow" variables and by introducing an effective potential. This innovative work created a new subject in physics, that is vibrational mechanics. Kapitza's method is used for description of periodic processes in [[atomic physics]], [[plasma physics]], [[cybernetical physics]]. The effective potential which describes the "slow" component of motion is described in "Mechanics" volume of the [[Lev Landau|Landau]]'s [[Course of Theoretical Physics]].<ref>{{cite book | |||
|author=[[Lev Landau|L.D. Landau]], [[Evgeny Lifshitz|E.M. Lifshitz]] | |||
|year=1960 | |||
|title=Mechanics | |||
|edition=1st |volume=Vol. 1 | |||
|publisher=[[Pergamon Press]] | |||
|isbn= | |||
|oclc= | |||
|asin=B0006AWV88 | |||
}}</ref> | |||
Another interesting feature of the Kapitza pendulum system is that the bottom equilibrium position, with the pendulum hanging down below the pivot, is no longer stable. Any tiny deviation from the vertical increases in amplitude with time.<ref>Бутиков Е. И. «Маятник с осциллирующим подвесом (к 60-летию маятника Капицы»), [http://faculty.ifmo.ru/butikov/Russian/ParamPendulum.pdf учебное пособие].</ref> Also [[parametric resonance]] can occur in this position, and [[Chaos theory|chaotic regimes]] can be realized in that system when [[strange attractor]]s are present in the [[Poincaré section]] . | |||
== Notation == | |||
[[File:KapitzaPendulumScheme.gif|thumb|240px|right|Kapitza's pendulum scheme]] | |||
Denote the vertical axis as <math>y</math> and the horizontal axis as <math>x</math> so that the motion of pendulum happens in the (<math>x</math>—<math>y</math>) plane. The following notation will be used | |||
* <math>\nu</math>—frequency of the vertical oscillations of the suspension, | |||
* <math>a</math> — amplitude of the oscillations of the suspension, | |||
* <math>\omega_0 = \sqrt{g/l}</math> — proper frequency of the mathematical pendulum, | |||
* <math>g</math> — free fall acceleration, | |||
* <math>l</math> — length of rigid and light pendulum, | |||
* <math>m</math> — mass. | |||
Denoting the angle between pendulum and downward direction as <math>\varphi</math> the time dependence of the position of pendulum gets written as | |||
<center><math>\begin{matrix} | |||
\left\{ | |||
\begin{matrix} | |||
x &=& l \sin \varphi\\ | |||
y &=& - l \cos \varphi - a \cos \nu t | |||
\end{matrix} \right. | |||
\end{matrix}</math></center> | |||
== Energy == | |||
The [[potential energy]] of the pendulum is due to gravity and is defined by of the vertical position as | |||
<center><math>\begin{matrix} | |||
E_{POT} = - m g (l \cos \varphi + a \cos \nu t)\;. | |||
\end{matrix}</math></center> | |||
The [[kinetic energy]] in addition to the standard term <math>E_{KIN}=m l^2 \dot \varphi^2 /2</math>, describing velocity of a mathematical pendulum, there is a contribution due to vibrations of the suspension | |||
<center><math>\begin{matrix} | |||
E_{KIN} | |||
= \frac{m l^2 }{2} \dot \varphi^2 + m a l \nu ~\sin(\nu t) \sin(\varphi)~\dot\varphi + \frac{m a^2 \nu^2}{2} \sin^2(\nu t)\;. | |||
\end{matrix}</math></center> | |||
The total energy is given by the sum of the kinetic and potential energies <math>E = E_{KIN} + E_{POT}</math> and the [[Lagrangian]] by their difference <math>L = E_{KIN} - E_{POT}</math>. | |||
The total energy is conserved in a mathematical pendulum, so time <math>t</math> dependence of the potential <math>E_{POT}</math> and kinetic <math>E_{KIN}</math> energies is symmetric with respect to the horizontal line. According to the [[virial theorem]] the mean kinetic and potential energies in harmonic oscillator are equal. This means that the line of symmetry corresponds to half of the total energy. | |||
In the case of vibrating suspension the system is no longer is a [[Closed system (thermodynamics)|closed one]] and the total energy is no longer conserved. The kinetic energy is more sensitive to vibration compared to the potential one. The potential energy <math>E_{POT} = mgy</math> is bound from below and above <math>-mg(l+a)<E_{POT}<mg(l+a)</math> while the kinetic energy is bound only from below <math>E_{KIN}\ge 0</math>. For high frequency of vibrations <math>\nu</math> the kinetic energy can be large compared to the potential energy. | |||
== Equations of motion == | |||
Motion of pendulum satisfies [[Euler-Lagrange equation]]s. The dependence of the phase <math>\varphi</math> of the pendulum on its position satisfies the equation:<ref>{{cite book | |||
|author=V.P. Krainov | |||
|year=2002 | |||
|title=Selected Mathematical Methods in Theoretical Physics | |||
|edition=1st | |||
|publisher=[[Taylor & Francis]] | |||
|isbn=978-0-415-27234-6 | |||
|oclc= | |||
}}</ref> | |||
<center><math>\begin{matrix} | |||
\frac{d}{dt} \frac{\partial L}{\partial \dot \varphi} = \frac{\partial L}{\partial \varphi}\;, | |||
\end{matrix}</math></center> | |||
where the Lagrangian <math>L</math> reads | |||
<center><math>\begin{matrix} | |||
L = \frac{m l^2 }{2} \dot \varphi^2 + ml( g + a~\nu^2\cos\nu t) \cos \varphi\;, | |||
\end{matrix}</math></center> | |||
up to irrelevant total time derivative terms. The differential equation | |||
<center><math>\begin{matrix} | |||
\ddot \varphi = - (g+a~\nu^2\cos\nu t) \frac{\sin \varphi}{l}\;, | |||
\end{matrix}</math></center> | |||
which describes the movement of the pendulum is nonlinear due to the <math>\sin\varphi</math> factor. The presence of the nonlinear term might lead to [[chaos theory|chaotic]] motion and to appearance of [[strange attractor]]s. | |||
== Equilibrium positions == | |||
Model of Kapitza's pendulum is more general than the model of mathematical pendulum. The latter is reproduced in the limit <math>a = 0</math>. Its [[phase portrait]] is a simple circle <math>x^2+y^2 = l^2 = const</math>. If the energy in the initial moment was larger than the maximum of the potential energy <math>E > mgl</math> then the trajectory will be closed and cyclic. If the initial energy is smaller <math>E < mgl</math> then the pendulum will oscillate close to the only stably point <math>(x,y) = (0,-l)</math>. | |||
When the suspension is vibrating with a small amplitude <math> a \ll l </math> and with a frequency <math>\nu\gg \omega_0 </math> much higher than the proper frequency <math>\omega_0</math>, the angle <math> \varphi</math> may be viewed as a superposition <math> \varphi=\varphi_0+\xi</math> of a "slow" component <math>\varphi_0</math> and a rapid oscillation <math>\xi</math> with small amplitude due to the small but rapid vibrations of the suspension. Technically, we perform a [[perturbative]] expansion in the "[[coupling constant]]s" <math> (a/l),(\omega_0/\nu) \ll 1 </math> while treating the ratio <math> (a/l)(\nu/\omega_0)</math> as fixed. The perturbative treatment becomes exact in the [[double scaling limit]] <math> a \to 0 ,\nu\to \infty</math>. More precisely, the rapid oscillation <math>\xi</math> is defined as | |||
<center><math>\begin{matrix} | |||
\xi = \frac{a}{l}\sin\varphi_0 ~\cos\nu t\;. | |||
\end{matrix}</math></center> | |||
The equation of motion for the "slow" component <math>\varphi_0</math> becomes | |||
<center><math>\begin{array}{rcl} | |||
\ddot\varphi_0 = \ddot\varphi - \ddot\xi &=& -(g+a~\nu^2\cos\nu t)\frac{\sin\varphi}{l} - \frac{a}{l}\left(\ddot\varphi_0 \cos \varphi_0 ~\cos\nu t -\dot\varphi_0^2\sin\varphi_0 ~\cos\nu t - 2\nu\dot\varphi_0\cos\varphi_0~\sin\nu t - \nu^2\sin \varphi_0 ~\cos\nu t \right) \\ | |||
&=& -\frac{g}{l}\sin\varphi_0 -(g+a~\nu^2\cos\nu t) \frac{1}{l}\left(\xi\cos\varphi_0 + O(\xi^2)\right) - \frac{a}{l}\left( \ddot\varphi_0 \cos\varphi_0 ~\cos\nu t -\dot\varphi_0^2\sin\varphi_0 ~\cos\nu t - 2\nu\dot\varphi_0\cos\varphi_0~\sin\nu t \right)\;. | |||
\end{array}</math></center> | |||
Time averaging over the rapid <math>\nu</math>-oscillation yields to leading order | |||
<center><math>\begin{matrix} | |||
\ddot \varphi_0 = - \frac{g}{l}\sin \varphi_0 - \frac{1}{2}(\frac{a\nu}{l})^2\sin \varphi_0 \cos \varphi_0 \;. | |||
\end{matrix}</math></center> | |||
The "slow" equation of motion becomes | |||
<center><math>\begin{matrix} | |||
m l^2\ddot \varphi_0 = -\frac{\partial V_{\mathrm{eff}}}{\partial \varphi_0} \;, | |||
\end{matrix}</math></center> | |||
by introducing an [[effective potential]] | |||
<center><math>\begin{matrix} | |||
V_{\mathrm{eff}} = - mgl \cos \varphi_0 + m (\frac{a\nu}{2}\sin \varphi_0)^2 \;. | |||
\end{matrix}</math></center> | |||
It turns out<ref name="Kapitza" /> that the effective potential <math> V_{\mathrm{eff}} </math> has two minima if <math>(a\nu)^2 > 2gl </math>, or equivalently, <math> (a/l)(\nu/\omega_0) > \sqrt{2} </math>. The first minimum is in the same position <math>(x,y)=(0,-l)</math> as the mathematical pendulum and the other minimum is in the upper vertical position <math>(x,y)=(0,l)</math>. As a result the upper vertical position, which is unstable in a mathematical pendulum, can become stable in Kapitza's pendulum. | |||
== Phase portrait == | |||
Interesting phase portraits might be obtained in regimes which are not accessible within analytic descriptions, for example in the case of large amplitude of the suspension <math>a \approx l</math>.<ref>G.E. Astrakharchik, N.A. Astrakharchik «Numerical study of Kapitza pendulum» [http://arxiv.org/pdf/1103.5981v1 arXiv:1103.5981 (2011)]</ref><ref> | |||
Time motion of Kapitza’s pendulum can be modeled in online java applets he sites | |||
http://www.myphysicslab.com/beta/Inverted-pendulum.html | |||
http://faculty.ifmo.ru/butikov/Nonlinear/index.html | |||
Arbitrary parameters of the system can be used and can be inserted manually.</ref> Increasing the amplitude of driving oscillations to half of the pendulum length <math>a = l/2</math> leads to the phase portrait shown in the figure. | |||
Further increase of the amplitude to <math>a\approx l</math>) leads to full filling of the internal points of the phase space, if before some points of the phase space were not accessible, now system can reach any of the internal points. This situation holds also for larger values of <math>a</math>. | |||
== Interesting facts == | |||
* Kapitza noted that a [[pendulum clock]] with a vibrating pendulum suspension always goes faster than a clock with a fixed suspension. | |||
* [[Walking]] is defined by an 'inverted pendulum' gait in which the body vaults over the stiff limb or limbs with each step. Increased stability during walking might be related to stability of Kapitza's pendulum. This applies regardless of the number of limbs - even arthropods with six, eight or more limbs. | |||
== Literature == | |||
{{Reflist}} | |||
{{DEFAULTSORT:Kapitza's Pendulum}} | |||
[[Category:Pendulums]] | |||
Revision as of 08:48, 30 January 2014

Kapitza's pendulum is a rigid pendulum in which the pivot point vibrates in a vertical direction, up and down. It is named after Russian Nobel laureate physicist Pyotr Kapitza, who in 1951 developed a theory which successfully explains some of its unusual properties.[1] The unique feature of the Kapitza pendulum is that the vibrating suspension can cause it to balance stably in an inverted position, with the bob above the suspension point. In the usual pendulum with a fixed suspension, the only stable equilibrium position is with the bob hanging below the suspension point; the inverted position is a point of unstable equilibrium, and the smallest perturbation moves the pendulum out of equilibrium. In nonlinear control theory the Kapitza pendulum is used as an example of a parametric oscillator that demonstrates the concept of "dynamic stabilization".
The pendulum was first described by A. Stephenson in 1908, who found that the upper vertical position of the pendulum might be stable when the driving frequency is fast[2] Yet until the 1950s there was no explanation for this highly unusual and counterintuitive phenomenon. Pyotr Kapitza was the first to analyze it in 1951.[1] He carried out a number of experimental studies and as well provided an analytical insight into the reasons of stability by splitting the motion into "fast" and "slow" variables and by introducing an effective potential. This innovative work created a new subject in physics, that is vibrational mechanics. Kapitza's method is used for description of periodic processes in atomic physics, plasma physics, cybernetical physics. The effective potential which describes the "slow" component of motion is described in "Mechanics" volume of the Landau's Course of Theoretical Physics.[3]
Another interesting feature of the Kapitza pendulum system is that the bottom equilibrium position, with the pendulum hanging down below the pivot, is no longer stable. Any tiny deviation from the vertical increases in amplitude with time.[4] Also parametric resonance can occur in this position, and chaotic regimes can be realized in that system when strange attractors are present in the Poincaré section .
Notation
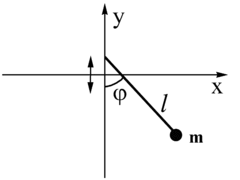
Denote the vertical axis as and the horizontal axis as so that the motion of pendulum happens in the (—) plane. The following notation will be used
- —frequency of the vertical oscillations of the suspension,
- — amplitude of the oscillations of the suspension,
- — proper frequency of the mathematical pendulum,
- — free fall acceleration,
- — length of rigid and light pendulum,
- — mass.
Denoting the angle between pendulum and downward direction as the time dependence of the position of pendulum gets written as
Energy
The potential energy of the pendulum is due to gravity and is defined by of the vertical position as
The kinetic energy in addition to the standard term , describing velocity of a mathematical pendulum, there is a contribution due to vibrations of the suspension
The total energy is given by the sum of the kinetic and potential energies and the Lagrangian by their difference .
The total energy is conserved in a mathematical pendulum, so time dependence of the potential and kinetic energies is symmetric with respect to the horizontal line. According to the virial theorem the mean kinetic and potential energies in harmonic oscillator are equal. This means that the line of symmetry corresponds to half of the total energy.
In the case of vibrating suspension the system is no longer is a closed one and the total energy is no longer conserved. The kinetic energy is more sensitive to vibration compared to the potential one. The potential energy is bound from below and above while the kinetic energy is bound only from below . For high frequency of vibrations the kinetic energy can be large compared to the potential energy.
Equations of motion
Motion of pendulum satisfies Euler-Lagrange equations. The dependence of the phase of the pendulum on its position satisfies the equation:[5]
up to irrelevant total time derivative terms. The differential equation
which describes the movement of the pendulum is nonlinear due to the factor. The presence of the nonlinear term might lead to chaotic motion and to appearance of strange attractors.
Equilibrium positions
Model of Kapitza's pendulum is more general than the model of mathematical pendulum. The latter is reproduced in the limit . Its phase portrait is a simple circle . If the energy in the initial moment was larger than the maximum of the potential energy then the trajectory will be closed and cyclic. If the initial energy is smaller then the pendulum will oscillate close to the only stably point .
When the suspension is vibrating with a small amplitude and with a frequency much higher than the proper frequency , the angle may be viewed as a superposition of a "slow" component and a rapid oscillation with small amplitude due to the small but rapid vibrations of the suspension. Technically, we perform a perturbative expansion in the "coupling constants" while treating the ratio as fixed. The perturbative treatment becomes exact in the double scaling limit . More precisely, the rapid oscillation is defined as
The equation of motion for the "slow" component becomes
Time averaging over the rapid -oscillation yields to leading order
The "slow" equation of motion becomes
by introducing an effective potential
It turns out[1] that the effective potential has two minima if , or equivalently, . The first minimum is in the same position as the mathematical pendulum and the other minimum is in the upper vertical position . As a result the upper vertical position, which is unstable in a mathematical pendulum, can become stable in Kapitza's pendulum.
Phase portrait
Interesting phase portraits might be obtained in regimes which are not accessible within analytic descriptions, for example in the case of large amplitude of the suspension .[6][7] Increasing the amplitude of driving oscillations to half of the pendulum length leads to the phase portrait shown in the figure.
Further increase of the amplitude to ) leads to full filling of the internal points of the phase space, if before some points of the phase space were not accessible, now system can reach any of the internal points. This situation holds also for larger values of .
Interesting facts
- Kapitza noted that a pendulum clock with a vibrating pendulum suspension always goes faster than a clock with a fixed suspension.
- Walking is defined by an 'inverted pendulum' gait in which the body vaults over the stiff limb or limbs with each step. Increased stability during walking might be related to stability of Kapitza's pendulum. This applies regardless of the number of limbs - even arthropods with six, eight or more limbs.
Literature
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ 1.0 1.1 1.2 P.L. Kapitza, “Dynamic stability of a pendulum when its point of suspension vibrates”, Soviet Phys. JETP 21, 588–592 (1951); P.L. Kapitza, “Pendulum with a vibrating suspension” Usp. Fiz. Nauk, 44, 7-15 (1951).
- ↑ A. Stephenson "On an induced stability" Phil. Mag. 15, 233 (1908). [1]
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ Бутиков Е. И. «Маятник с осциллирующим подвесом (к 60-летию маятника Капицы»), учебное пособие.
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ G.E. Astrakharchik, N.A. Astrakharchik «Numerical study of Kapitza pendulum» arXiv:1103.5981 (2011)
- ↑ Time motion of Kapitza’s pendulum can be modeled in online java applets he sites http://www.myphysicslab.com/beta/Inverted-pendulum.html http://faculty.ifmo.ru/butikov/Nonlinear/index.html Arbitrary parameters of the system can be used and can be inserted manually.


















































