Pierre Raymond de Montmort

Template:Continuum mechanics A neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, the stress-strain curve of a neo-Hookean material is not linear. Instead, the relationship between applied stress and strain is initially linear, but at a certain point the stress-strain curve will plateau. The neo-Hookean model does not account for the dissipative release of energy as heat while straining the material and perfect elasticity is assumed at all stages of deformation.

The neo-Hookean model is based on the statistical thermodynamics of cross-linked polymer chains and is usable for plastics and rubber-like substances. Cross-linked polymers will act in a neo-Hookean manner because initially the polymer chains can move relative to each other when a stress is applied. However, at a certain point the polymer chains will be stretched to the maximum point that the covalent cross links will allow, and this will cause a dramatic increase in the elastic modulus of the material. The neo-Hookean material model does not predict that increase in modulus at large strains and is typically accurate only for strains less than 20%. The model is also inadequate for biaxial states of stress and has been superseded by the Mooney-Rivlin model.

The strain energy density function for an incompressible neo-Hookean material is

$W=C_1(I_1-3)$

where $C_1$ is a material constant, and $I_1$ is the first invariant of the left Cauchy-Green deformation tensor, i.e.,

$I_1={\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2$

where ${\lambda }_i$ are the principal stretches. For three-dimensional problems the compressible neo-Hookean material the strain energy density function is given by

$W=C_1({\overline{I}}_1-3)+D_1(J-1{)}^2;J=\det (\mathit{F})={\lambda }_1{\lambda }_2{\lambda }_3$

where $D_1$ is a material constant, ${\overline{I}}_1=J^{-2/3}{I}_1$ is the first invariant of the deviatoric part of the left Cauchy-Green deformation tensor, and $\mathit{F}$ is the deformation gradient. It can be shown that in 2D, the strain energy density function now becomes

$W=C_1({\overline{I}}_1-2)+D_1(J-1{)}^2;$

where ${\overline{I}}_1=I_1/J$.

Several alternative formulations exist for compressible neo-Hookean materials, for example

$W=C_1({\overline{I}}_1-3-2\ln J)+D_1(J-1{)}^2$

For consistency with linear elasticity,

$C_1=\frac{\mu }{2};D_1=\frac{\kappa }{2}$

where $\mu$ is the shear modulus and $\kappa$ is the bulk modulus.

Cauchy stress in terms of deformation tensors

Compressible neo-Hookean material

For a compressible Rivlin neo-Hookean material the Cauchy stress is given by

$J\mathit{\sigma }=-p\mathit{1}+2C_1\mathrm{d}\mathrm{e}\mathrm{v}(\overline{\mathit{B}})=-p\mathit{1}+\frac{2C_1}{J^{2/3}}\mathrm{d}\mathrm{e}\mathrm{v}(\mathit{B})$

where $\mathit{B}$ is the left Cauchy-Green deformation tensor, and

$p:=-2D_{1}J(J-1);\mathrm{d}\mathrm{e}\mathrm{v}(\overline{\mathit{B}})=\overline{\mathit{B}}-\frac{1}{3}{\overline{I}}_1\mathit{1};\overline{\mathit{B}}=J^{-2/3}\mathit{B}.$

For infinitesimal strains ($\mathit{\epsilon }$)

$J\approx 1+\mathrm{t}\mathrm{r}(\mathit{\epsilon });\mathit{B}\approx \mathit{1}+2\mathit{\epsilon }$

and the Cauchy stress can be expressed as

$\mathit{\sigma }\approx 4C_1(\mathit{\epsilon }-\frac{1}{3}\mathrm{t}\mathrm{r}(\mathit{\epsilon })\mathit{1})+2D_1\mathrm{t}\mathrm{r}(\mathit{\epsilon })\mathit{1}$

Comparison with Hooke's law shows that $\mu =2C_1$ and $\kappa =2D_1$.

Proof:

The Cauchy stress in a compressible hyperelastic material is given by $\mathit{\sigma }=\frac{2}{J}[\frac{1}{J^{2/3}}(\frac{\partial W}{\partial {\overline{I}}_1}+{\overline{I}}_1\frac{\partial W}{\partial {\overline{I}}_2})\mathit{B}-\frac{1}{J^{4/3}}\frac{\partial W}{\partial {\overline{I}}_2}\mathit{B}\cdot \mathit{B}]+[\frac{\partial W}{\partial J}-\frac{2}{3J}({\overline{I}}_1\frac{\partial W}{\partial {\overline{I}}_1}+2{\overline{I}}_2\frac{\partial W}{\partial {\overline{I}}_2})]\mathit{1}$ For a compressible Rivlin neo-Hookean material, $\frac{\partial W}{\partial {\overline{I}}_1}=C_1;\frac{\partial W}{\partial {\overline{I}}_2}=0;\frac{\partial W}{\partial J}=2D_1(J-1)$ while, for a compressible Ogden neo-Hookean material, $\frac{\partial W}{\partial {\overline{I}}_1}=C_1;\frac{\partial W}{\partial {\overline{I}}_2}=0;\frac{\partial W}{\partial J}=2D_1(J-1)-\frac{2C_1}{J}$ Therefore, the Cauchy stress in a compressible Rivlin neo-Hookean material is given by $\mathit{\sigma }=\frac{2}{J}\left[\frac{1}{J^{2/3}}{C}_1\mathit{B}\right]+[2D_1(J-1)-\frac{2}{3J}{C}_1{\overline{I}}_1]\mathit{1}$ while that for the corresponding Ogden material is $\mathit{\sigma }=\frac{2}{J}\left[\frac{1}{J^{2/3}}{C}_1\mathit{B}\right]+[2D_1(J-1)-\frac{2C_1}{J}-\frac{2}{3J}{C}_1{\overline{I}}_1]\mathit{1}$ If the isochoric part of the left Cauchy-Green deformation tensor is defined as $\overline{\mathit{B}}=J^{-2/3}\mathit{B}$, then we can write the Rivlin neo-Heooken stress as $\mathit{\sigma }=\frac{2C_1}{J}[\overline{\mathit{B}}-\frac{1}{3}{\overline{I}}_1\mathit{1}]+2D_1(J-1)\mathit{1}=\frac{2C_1}{J}\mathrm{d}\mathrm{e}\mathrm{v}(\overline{\mathit{B}})+2D_1(J-1)\mathit{1}$ and the Ogden neo-Hookean stress as $\mathit{\sigma }=\frac{2C_1}{J}[\overline{\mathit{B}}-\frac{1}{3}{\overline{I}}_1\mathit{1}-\mathit{1}]+2D_1(J-1)\mathit{1}=\frac{2C_1}{J}[\mathrm{d}\mathrm{e}\mathrm{v}(\overline{\mathit{B}})-\mathit{1}]+2D_1(J-1)\mathit{1}$ The quantities $p:=-2D_{1}J(J-1);p^{*}=-2D_{1}J(J-1)+2C_1$ have the form of pressures and are usually treated as such. The Rivlin neo-Hookean stress can then be expressed in the form $\mathit{\tau }=J\mathit{\sigma }=-p\mathit{1}+2C_1\mathrm{d}\mathrm{e}\mathrm{v}(\overline{\mathit{B}})$ while the Ogden neo-Hookean stress has the form $\mathit{\tau }=-p^{*}\mathit{1}+2C_1\mathrm{d}\mathrm{e}\mathrm{v}(\overline{\mathit{B}})$

Incompressible neo-Hookean material

For an incompressible neo-Hookean material with $J=1$

$\mathit{\sigma }=-p\mathit{1}+2C_1\mathit{B}$

where $p$ is an undetermined pressure.

Cauchy stress in terms of principal stretches

Compressible neo-Hookean material

For a compressible neo-Hookean hyperelastic material, the principal components of the Cauchy stress are given by

${\sigma }_i=2C_1{J}^{-5/3}[{\lambda }_i^2-\frac{I_1}{3}]+2D_1(J-1);i=1,2,3$

Therefore, the differences between the principal stresses are

${\sigma }_{11}-{\sigma }_{33}=\frac{2C_1}{J^{5/3}}({\lambda }_1^2-{\lambda }_3^2);{\sigma }_{22}-{\sigma }_{33}=\frac{2C_1}{J^{5/3}}({\lambda }_2^2-{\lambda }_3^2)$

Proof:

For a compressible hyperelastic material, the principal components of the Cauchy stress are given by ${\sigma }_i=\frac{{\lambda }_i}{{\lambda }_1{\lambda }_2{\lambda }_3}\frac{\partial W}{\partial {\lambda }_i};i=1,2,3$ The strain energy density function for a compressible neo Hookean material is $W=C_1({\overline{I}}_1-3)+D_1(J-1{)}^2=C_1[J^{-2/3}({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)-3]+D_1(J-1{)}^2$ Therefore, ${\lambda }_i\frac{\partial W}{\partial {\lambda }_i}=C_1[-\frac{2}{3}{J}^{-5/3}{\lambda }_i\frac{\partial J}{\partial {\lambda }_i}({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)+2J^{-2/3}{\lambda }_i^2]+2D_1(J-1){\lambda }_i\frac{\partial J}{\partial {\lambda }_i}$ Since $J={\lambda }_1{\lambda }_2{\lambda }_3$ we have ${\lambda }_i\frac{\partial J}{\partial {\lambda }_i}={\lambda }_1{\lambda }_2{\lambda }_3=J$ Hence, $\begin{array}{rl}{\lambda }_i\frac{\partial W}{\partial {\lambda }_i}& =C_1[-\frac{2}{3}{J}^{-2/3}({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)+2J^{-2/3}{\lambda }_i^2]+2D_{1}J(J-1)\\ & =2C_1{J}^{-2/3}[-\frac{1}{3}({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2)+{\lambda }_i^2]+2D_{1}J(J-1)\end{array}$ The principal Cauchy stresses are therefore given by ${\sigma }_i=2C_1{J}^{-5/3}[{\lambda }_i^2-\frac{I_1}{3}]+2D_1(J-1)$

Incompressible neo-Hookean material

In terms of the principal stretches, the Cauchy stress differences for an incompressible hyperelastic material are given by

${\sigma }_{11}-{\sigma }_{33}={\lambda }_1\frac{\partial W}{\partial {\lambda }_1}-{\lambda }_3\frac{\partial W}{\partial {\lambda }_3};{\sigma }_{22}-{\sigma }_{33}={\lambda }_2\frac{\partial W}{\partial {\lambda }_2}-{\lambda }_3\frac{\partial W}{\partial {\lambda }_3}$

For an incompressible neo-Hookean material,

$W=C_1({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-3);{\lambda }_1{\lambda }_2{\lambda }_3=1$

Therefore,

$\frac{\partial W}{\partial {\lambda }_1}=2C_1{\lambda }_1;\frac{\partial W}{\partial {\lambda }_2}=2C_1{\lambda }_2;\frac{\partial W}{\partial {\lambda }_3}=2C_1{\lambda }_3$

which gives

${\sigma }_{11}-{\sigma }_{33}=2({\lambda }_1^2-{\lambda }_3^2)C_1;{\sigma }_{22}-{\sigma }_{33}=2({\lambda }_2^2-{\lambda }_3^2)C_1$

Uniaxial extension

Compressible neo-Hookean material

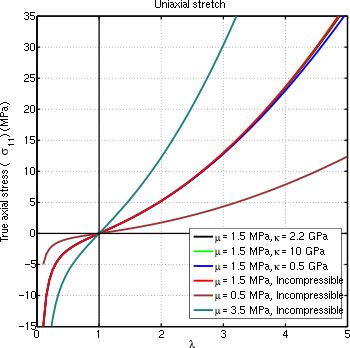
The true stress as a function of uniaxial stretch predicted by a compressible neo-Hookean material for various values of $C_1,D_1$. The material properties are representative of natural rubber.

For a compressible material undergoing uniaxial extension, the principal stretches are

${\lambda }_1=\lambda ;{\lambda }_2={\lambda }_3=\sqrt{\frac{J}{\lambda }};I_1={\lambda }^2+\frac{2J}{\lambda }$

Hence, the true (Cauchy) stresses for a compressible neo-Hookean material are given by

$\begin{array}{rl}{\sigma }_{11}& =\frac{4C_1}{3J^{5/3}}({\lambda }^2-\frac{J}{\lambda })+2D_1(J-1)\\ {\sigma }_{22}& ={\sigma }_{33}=\frac{2C_1}{3J^{5/3}}(\frac{J}{\lambda }-{\lambda }^2)+2D_1(J-1)\end{array}$

The stress differences are given by

${\sigma }_{11}-{\sigma }_{33}=\frac{2C_1}{J^{5/3}}({\lambda }^2-\frac{J}{\lambda });{\sigma }_{22}-{\sigma }_{33}=0$

If the material is unconstrained we have ${\sigma }_{22}={\sigma }_{33}=0$. Then

${\sigma }_{11}=\frac{2C_1}{J^{5/3}}({\lambda }^2-\frac{J}{\lambda })$

Equating the two expressions for ${\sigma }_{11}$ gives a relation for $J$ as a function of $\lambda$, i.e.,

$\frac{4C_1}{3J^{5/3}}({\lambda }^2-\frac{J}{\lambda })+2D_1(J-1)=\frac{2C_1}{J^{5/3}}({\lambda }^2-\frac{J}{\lambda })$

or

$D_1{J}^{8/3}-D_1{J}^{5/3}+\frac{C_1}{3\lambda }J-\frac{C_1{\lambda }^2}{3}=0$

The above equation can be solved numerically using a Newton-Raphson iterative root finding procedure.

Incompressible neo-Hookean material

Comparison of experimental results (dots) and predictions for Hooke's law(1), neo-Hookean solid(2) and Mooney-Rivlin solid models(3)

Under uniaxial extension, ${\lambda }_1=\lambda$ and ${\lambda }_2={\lambda }_3=1/\sqrt{\lambda }$. Therefore,

${\sigma }_{11}-{\sigma }_{33}=2C_1({\lambda }^2-\frac{1}{\lambda });{\sigma }_{22}-{\sigma }_{33}=0$

Assuming no traction on the sides, ${\sigma }_{22}={\sigma }_{33}=0$, so we can write

${\sigma }_{11}=2C_1({\lambda }^2-\frac{1}{\lambda })=2C_1\left(\frac{3{\epsilon }_{11}+3{\epsilon }_{11}^2+{\epsilon }_{11}^3}{1+{\epsilon }_{11}}\right)$

where ${\epsilon }_{11}=\lambda -1$ is the engineering strain. This equation is often written in alternative notation as

$T_{11}=2C_1({\alpha }^2-\frac{1}{\alpha })$

The equation above is for the true stress (ratio of the elongation force to deformed cross-section). For the engineering stress the equation is:

${\sigma }_{11}^{\mathrm{e}\mathrm{n}\mathrm{g}}=2C_1(\lambda -\frac{1}{{\lambda }^2})$

For small deformations $\epsilon \ll 1$ we will have:

${\sigma }_{11}=6C_1\epsilon =3\mu \epsilon$

Thus, the equivalent Young's modulus of a neo-Hookean solid in uniaxial extension is $3\mu$, which is in concordance with linear elasticity ($E=2\mu (1+\nu )$ with $\nu =0.5$ for incompressibility).

Equibiaxial extension

Compressible neo-Hookean material

The true stress as a function of biaxial stretch predicted by a compressible neo-Hookean material for various values of $C_1,D_1$. The material properties are representative of natural rubber.

In the case of equibiaxial extension

${\lambda }_1={\lambda }_2=\lambda ;{\lambda }_3=\frac{J}{{\lambda }^2};I_1=2{\lambda }^2+\frac{J^2}{{\lambda }^4}$

Therefore,

$\begin{array}{rl}{\sigma }_{11}& =2C_1[\frac{{\lambda }^2}{J^{5/3}}-\frac{1}{3J}(2{\lambda }^2+\frac{J^2}{{\lambda }^4})]+2D_1(J-1)\\ & ={\sigma }_{22}\\ {\sigma }_{33}& =2C_1[\frac{J^{1/3}}{{\lambda }^4}-\frac{1}{3J}(2{\lambda }^2+\frac{J^2}{{\lambda }^4})]+2D_1(J-1)\end{array}$

The stress differences are

${\sigma }_{11}-{\sigma }_{22}=0;{\sigma }_{11}-{\sigma }_{33}=\frac{2C_1}{J^{5/3}}({\lambda }^2-\frac{J^2}{{\lambda }^4})$

If the material is in a state of plane stress then ${\sigma }_{33}=0$ and we have

${\sigma }_{11}={\sigma }_{22}=\frac{2C_1}{J^{5/3}}({\lambda }^2-\frac{J^2}{{\lambda }^4})$

We also have a relation between $J$ and $\lambda$:

$2C_1[\frac{{\lambda }^2}{J^{5/3}}-\frac{1}{3J}(2{\lambda }^2+\frac{J^2}{{\lambda }^4})]+2D_1(J-1)=\frac{2C_1}{J^{5/3}}({\lambda }^2-\frac{J^2}{{\lambda }^4})$

or,

$(2D_1-\frac{C_1}{{\lambda }^4})J^2+\frac{3C_1}{{\lambda }^4}{J}^{4/3}-3D_{1}J-2C_1{\lambda }^2=0$

This equation can be solved for $J$ using Newton's method.

Incompressible neo-Hookean material

For an incompressible material $J=1$ and the differences between the principal Cauchy stresses take the form

${\sigma }_{11}-{\sigma }_{22}=0;{\sigma }_{11}-{\sigma }_{33}=2C_1({\lambda }^2-\frac{1}{{\lambda }^4})$

Under plane stress conditions we have

${\sigma }_{11}=2C_1({\lambda }^2-\frac{1}{{\lambda }^4})$

Pure dilation

For the case of pure dilation

${\lambda }_1={\lambda }_2={\lambda }_3=\lambda :J={\lambda }^3;I_1=3{\lambda }^2$

Therefore, the principal Cauchy stresses for a compressible neo-Hookean material are given by

${\sigma }_i=2C_1(\frac{1}{{\lambda }^3}-\frac{1}{\lambda })+2D_1({\lambda }^3-1)$

If the material is incompressible then ${\lambda }^3=1$ and the principal stresses can be arbitrary.

The figures below show that extremely high stresses are needed to achieve large triaxial extensions or compressions. Equivalently, relatively small triaxial stretch states can cause very high stresses to develop in a rubber-like material. Note also that the magnitude of the stress is quite sensitive to the bulk modulus but not to the shear modulus.

The true stress as a function of equi-triaxial stretch predicted by a compressible neo-Hookean material for various values of $C_1,D_1$. The material properties are representative of natural rubber.

The true stress as a function of J predicted by a compressible neo-Hookean material for various values of $C_1,D_1$. The material properties are representative of natural rubber.

Simple shear

For the case of simple shear the deformation gradient in terms of components with respect to a reference basis is of the form

$\mathit{F}=\left[\begin{array}{ccc}1& \gamma & 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$

where $\gamma$ is the shear deformation. Therefore the left Cauchy-Green deformation tensor is

$\mathit{B}=\mathit{F}\cdot {\mathit{F}}^T=\left[\begin{array}{ccc}1+{\gamma }^2& \gamma & 0\\ \gamma & 1& 0\\ 0& 0& 1\end{array}\right]$

Compressible neo-Hookean material

In this case $J=\det (\mathit{F})=1$. Hence, $\mathit{\sigma }=2C_1\mathrm{d}\mathrm{e}\mathrm{v}(\mathit{B})$. Now,

$\mathrm{d}\mathrm{e}\mathrm{v}(\mathit{B})=\mathit{B}-\frac{1}{3}\mathrm{t}\mathrm{r}(\mathit{B})\mathit{1}=\mathit{B}-\frac{1}{3}(3+{\gamma }^2)\mathit{1}=\left[\begin{array}{ccc}\frac{2}{3}{\gamma }^2& \gamma & 0\\ \gamma & -\frac{1}{3}{\gamma }^2& 0\\ 0& 0& -\frac{1}{3}{\gamma }^2\end{array}\right]$

Hence the Cauchy stress is given by

$\mathit{\sigma }=\left[\begin{array}{ccc}\frac{4C_1}{3}{\gamma }^2& 2C_1\gamma & 0\\ 2C_1\gamma & -\frac{2C_1}{3}{\gamma }^2& 0\\ 0& 0& -\frac{2C_1}{3}{\gamma }^2\end{array}\right]$

Incompressible neo-Hookean material

Using the relation for the Cauchy stress for an incompressible neo-Hookean material we get

$\mathit{\sigma }=-p\mathit{1}+2C_1\mathit{B}=\left[\begin{array}{ccc}2C_1(1+{\gamma }^2)-p& 2C_1\gamma & 0\\ 2C_1\gamma & 2C_1-p& 0\\ 0& 0& 2C_1-p\end{array}\right]$

Thus neo-Hookean solid shows linear dependence of shear stresses upon shear deformation and quadratic dependence of the normal stress difference on the shear deformation. Note that the expressions for the Cauchy stress for a compressible and an incompressible neo-Hookean material in simple shear represent the same quantity and provide a means of determining the unknown pressure $p$.

See also

• Hyperelastic material
• Strain energy density function
• Mooney-Rivlin solid
• Finite strain theory
• Stress measures