Abel transform: Difference between revisions
en>Mark Arsten m Reverted edits by 130.212.142.18 (talk) to last revision by Fgnievinski (HG) |
|||
| Line 1: | Line 1: | ||
{{distinguish|Coefficient of variation}} | |||
[[File:Okuns law quarterly differences.svg|300px|thumb|[[Ordinary least squares]] regression of [[Okun's law]]. Since the regression line does not miss any of the points by very much, the ''R''<sup>2</sup> of the regression is relatively high.]] | |||
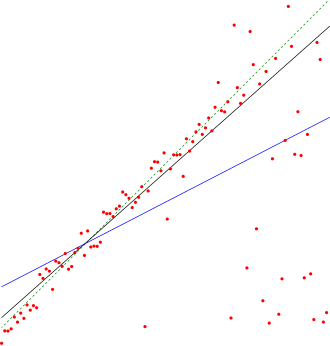
[[File:Thiel-Sen estimator.svg|thumb|Comparison of the [[Theil–Sen estimator]] (black) and [[simple linear regression]] (blue) for a set of points with [[outlier]]s. Because of the many outliers, neither of the regression lines fits the data well, as measured by the fact that neither gives a very high ''R''<sup>2</sup>.]] | |||
In [[statistics]], the '''coefficient of determination''', denoted '''''R''<sup>2</sup>''' and pronounced '''R squared''', indicates how well data points fits a statistical model – sometimes simply a line or curve. It is a [[statistic]] used in the context of [[statistical model]]s whose main purpose is either the [[Prediction#Statistics|prediction]] of future outcomes or the testing of [[hypotheses]], on the basis of other related information. It provides a measure of how well observed outcomes are replicated by the model, as the proportion of total variation of outcomes explained by the model.<ref>Steel, R.G.D, and Torrie, J. H., ''Principles and Procedures of Statistics with Special Reference to the Biological Sciences.'', [[McGraw Hill]], 1960, pp. 187, 287.)</ref> | |||
There are several different definitions of ''R''<sup>2</sup> which are only sometimes equivalent. One class of such cases includes that of [[simple linear regression]]. In this case, if an intercept is included then ''R''<sup>2</sup> is simply the square of the sample [[Pearson product-moment correlation coefficient|correlation coefficient]] between the outcomes and their predicted values; in the case of [[simple linear regression]], it is the square of the correlation between the outcomes and the values of the single regressor being used for prediction. If an intercept is included and the number of explanators is more than one, ''R''<sup>2</sup> is the square of the [[coefficient of multiple correlation]]. In such cases, the coefficient of determination ranges from 0 to 1. Important cases where the computational definition of ''R''<sup>2</sup> can yield negative values, depending on the definition used, arise where the predictions which are being compared to the corresponding outcomes have not been derived from a model-fitting procedure using those data, and where linear regression is conducted without including an intercept. Additionally, negative values of ''R''<sup>2</sup> may occur when fitting non-linear functions to data.<ref>{{cite journal |doi=10.1016/S0304-4076(96)01818-0 |title=An R-squared measure of goodness of fit for some common nonlinear regression models |year=1997 |last1=Colin Cameron |first1=A. |last2=Windmeijer |first2=Frank A.G. |journal=Journal of Econometrics |volume=77 |issue=2 |pmid=11230695 |pages=1790–2 |last3=Gramajo |first3=H |last4=Cane |first4=DE |last5=Khosla |first5=C}}</ref> In cases where negative values arise, the mean of the data provides a better fit to the outcomes than do the fitted function values, according to this particular criterion.<ref>{{cite web|last=Imdadullah|first=Muhammad|title=Coefficient of Determination|url=http://itfeature.com/correlation-and-regression-analysis/coefficient-of-determination|work=itfeature.com}}</ref> | |||
==Definitions== | |||
[[File:Coefficient of Determination.svg|thumb|400px|<math>R^2 = 1 - \frac{\color{blue}{SS_\text{res}}}{\color{red}{SS_\text{tot}}}</math><br> | |||
The better the linear regression (on the right) fits the data in comparison to the simple average (on the left graph), the closer the value of <math>R^2</math> is to one. The areas of the blue squares represent the squared residuals with respect to the linear regression. The areas of the red squares represent the squared residuals with respect to the average value.]] | |||
A data set has values ''y<sub>i</sub>'', each of which has an associated modelled value ''f<sub>i</sub>'' (also sometimes referred to as ''ŷ<sub>i</sub>''). Here, the values ''y<sub>i</sub>'' are called the observed values and the modelled values ''f<sub>i</sub>'' are sometimes called the predicted values. | |||
In what follows <math>\bar{y}</math> is the mean of the observed data: | |||
:<math>\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i </math> | |||
where ''n'' is the number of observations. | |||
The "variability" of the data set is measured through different [[sum of squares|sums of squares]]:{{disambiguation needed|date=December 2013}} | |||
: <math>SS_\text{tot}=\sum_i (y_i-\bar{y})^2,</math> the [[total sum of squares]] (proportional to the sample variance); | |||
:<math>SS_\text{reg}=\sum_i (f_i -\bar{y})^2,</math> the regression sum of squares, also called the [[explained sum of squares]]. | |||
:<math>SS_\text{res}=\sum_i (y_i - f_i)^2\,</math>, the sum of squares of residuals, also called the [[residual sum of squares]]. | |||
The notations <math>SS_{R}</math> and <math>SS_{E}</math> should be avoided, since in some texts their meaning is reversed to '''R'''esidual sum of squares and '''E'''xplained sum of squares, respectively. | |||
The most general definition of the coefficient of determination is | |||
:<math>R^2 \equiv 1 - {SS_{\rm res}\over SS_{\rm tot}}.\,</math> | |||
===Relation to unexplained variance=== | |||
In a general form, ''R''<sup>2</sup> can be seen to be related to the unexplained variance, since the second term compares the unexplained variance (variance of the model's errors) with the total variance (of the data). See [[fraction of variance unexplained]]. | |||
===As explained variance=== | |||
In some cases the [[total sum of squares]] equals the sum of the two other sums of squares defined above, | |||
:<math>SS_{\rm res}+SS_{\rm reg}=SS_{\rm tot}. \,</math> | |||
See [[Explained sum of squares#Partitioning in the general OLS model|partitioning in the general OLS model]] for a derivation of this result for one case where the relation holds. When this relation does hold, the above definition of ''R''<sup>2</sup> is equivalent to | |||
:<math>R^{2} = {SS_{\rm reg} \over SS_{\rm tot} } = {SS_{\rm reg}/n \over SS_{\rm tot}/n }.</math> | |||
In this form ''R''<sup>2</sup> is expressed as the ratio of the [[explained variation|explained variance]] (variance of the model's predictions, which is ''SS''<sub>reg</sub> / ''n'') to the total variance (sample variance of the dependent variable, which is ''SS''<sub>tot</sub> / ''n''). | |||
This partition of the sum of squares holds for instance when the model values ƒ<sub>''i''</sub> have been obtained by [[linear regression]]. A milder [[sufficient condition]] reads as follows: The model has the form | |||
:<math>f_i=\alpha+\beta q_i \,</math> | |||
where the ''q''<sub>''i''</sub> are arbitrary values that may or may not depend on ''i'' or on other free parameters (the common choice ''q''<sub>''i''</sub> = ''x''<sub>''i''</sub> is just one special case), and the coefficients α and β are obtained by minimizing the residual sum of squares. | |||
This set of conditions is an important one and it has a number of implications for the properties of the fitted [[Errors and residuals in statistics|residuals]] and the modelled values. In particular, under these conditions: | |||
:<math>\bar{f}=\bar{y}.\,</math> | |||
===As squared correlation coefficient=== | |||
Similarly, in linear least squares regression with an estimated intercept term, ''R''<sup>2</sup> equals the square of the [[Pearson product-moment correlation coefficient|Pearson correlation coefficient]] between the observed and modeled (predicted) data values of the dependent variable. | |||
Under more general modeling conditions, where the predicted values might be generated from a model different than linear least squares regression, an ''R''<sup>2</sup> value can be calculated as the square of the [[Pearson product-moment correlation coefficient|correlation coefficient]] between the original and modeled data values. In this case, the value is not directly a measure of how good the modeled values are, but rather a measure of how good a predictor might be constructed from the modeled values (by creating a revised predictor of the form α + βƒ<sub>''i''</sub>). According to Everitt (2002, p. 78), this usage is specifically the definition of the term "coefficient of determination": the square of the correlation between two (general) variables. | |||
==Interpretation== | |||
''R''<sup>2</sup> is a statistic that will give some information about the [[goodness of fit]] of a model. In regression, the ''R''<sup>2</sup> coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An ''R''<sup>2</sup> of 1 indicates that the regression line perfectly fits the data. | |||
Values of ''R''<sup>2</sup> outside the range 0 to 1 can occur where it is used to measure the agreement between observed and modeled values and where the "modeled" values are not obtained by linear regression and depending on which formulation of ''R''<sup>2</sup> is used. If the first formula above is used, values can be greater than one. If the second expression is used, there are no constraints on the values obtainable. | |||
In many (but not all) instances where ''R''<sup>2</sup> is used, the predictors are calculated by ordinary [[least-squares]] regression: that is, by minimizing ''SS''<sub>err</sub>. In this case ''R''<sup>2</sup> increases as we increase the number of variables in the model (''R''<sup>2</sup> is [[Monotonic function|monotone increasing]] with the number of variables included, i.e. it will never decrease). This illustrates a drawback to one possible use of ''R''<sup>2</sup>, where one might keep adding variables ([[Kitchen sink regression]]) to increase the ''R''<sup>2</sup> value. For example, if one is trying to predict the sales of a model of car from the car's gas mileage, price, and engine power, one can include such irrelevant factors as the first letter of the model's name or the height of the lead engineer designing the car because the ''R''<sup>2</sup> will never decrease as variables are added and will probably experience an increase due to chance alone. | |||
This leads to the alternative approach of looking at the [[#Adjusted R2|adjusted ''R''<sup>2</sup>]]. The explanation of this statistic is almost the same as ''R''<sup>2</sup> but it penalizes the statistic as extra variables are included in the model. For cases other than fitting by ordinary least squares, the ''R''<sup>2</sup> statistic can be calculated as above and may still be a useful measure. If fitting is by [[weighted least squares]] or [[generalized least squares]], alternative versions of R<sup>2</sup> can be calculated appropriate to those statistical frameworks, while the "raw" ''R''<sup>2</sup> may still be useful if it is more easily interpreted. Values for ''R''<sup>2</sup> can be calculated for any type of predictive model, which need not have a statistical basis. | |||
===In a linear model=== | |||
Consider a linear model of the form | |||
:<math>{Y_i = \beta_0 + \sum_{j=1}^p {\beta_j X_{i,j}} + \varepsilon_i},</math> | |||
where, for the ''i''th case, <math>{Y_i}</math> is the response variable, <math>X_{i,1},\dots,X_{i,p}</math> are ''p'' regressors, and <math>\varepsilon_i</math> is a mean zero [[errors and residuals in statistics|error]] term. The quantities <math>\beta_0,\dots,\beta_p</math> are unknown coefficients, whose values are estimated by [[least squares]]. The coefficient of determination ''R''<sup>2</sup> is a measure of the global fit of the model. Specifically, ''R''<sup>2</sup> is an element of [0, 1] and represents the proportion of variability in ''Y''<sub>''i''</sub> that may be attributed to some linear combination of the regressors ([[explanatory variable]]s) in ''X''. | |||
''R''<sup>2</sup> is often interpreted as the proportion of response variation "explained" by the regressors in the model. Thus, ''R''<sup>2</sup> = 1 indicates that the fitted model explains all variability in <math>y</math>, while ''R''<sup>2</sup> = 0 indicates no 'linear' relationship (for straight line regression, this means that the straight line model is a constant line (slope = 0, intercept = <math>\bar{y}</math>) between the response variable and regressors). An interior value such as ''R''<sup>2</sup> = 0.7 may be interpreted as follows: "Seventy percent of the variation in the response variable can be explained by the explanatory variables. The remaining thirty percent can be attributed to unknown, [[lurking variable]]s or inherent variability." | |||
A caution that applies to ''R''<sup>2</sup>, as to other statistical descriptions of [[correlation]] and association is that "[[correlation does not imply causation]]." In other words, while correlations may provide valuable clues regarding causal relationships among variables, a high correlation between two variables does not represent adequate evidence that changing one variable has resulted, or may result, from changes of other variables. | |||
In case of a single regressor, fitted by least squares, ''R''<sup>2</sup> is the square of the [[Pearson product-moment correlation coefficient]] relating the regressor and the response variable. More generally, ''R''<sup>2</sup> is the square of the correlation between the constructed predictor and the response variable. With more than one regressor, the ''R''<sup>2</sup> can be referred to as the [[coefficient of multiple determination]]. | |||
===Inflation of ''R''<sup>2</sup>=== | |||
In [[least squares]] regression, ''R''<sup>2</sup> is weakly increasing with increases in the number of regressors in the model. Because increases in the number of regressors increase the value of ''R''<sup>2</sup>, ''R''<sup>2</sup> alone cannot be used as a meaningful comparison of models with very different numbers of independent variables. For a meaningful comparison between two models, an [[F-test]] can be performed on the [[residual sum of squares]], similar to the F-tests in [[Granger causality]], though this is not always appropriate. As a reminder of this, some authors denote ''R''<sup>2</sup> by ''R''<sub>''p''</sub><sup>2</sup>, where ''p'' is the number of columns in ''X'' (the number of explanators including the constant). | |||
To demonstrate this property, first recall that the objective of least squares linear regression is: | |||
:<math>\min_b SS_\text{err}(b) \Rightarrow \min_b \sum_i (y_i - X_ib)^2\,</math> | |||
The optimal value of the objective is weakly smaller as additional columns of <math>X</math> are added, by the fact that less constrained minimization leads to an optimal cost which is weakly smaller than more constrained minimization does. Given the previous conclusion and noting that <math>SS_{tot}</math> depends only on ''y'', the non-decreasing property of ''R''<sup>2</sup> follows directly from the definition above. | |||
The intuitive reason that using an additional explanatory variable cannot lower the ''R''<sup>2</sup> is this: Minimizing <math>SS_\text{err}</math> is equivalent to maximizing ''R''<sup>2</sup>. When the extra variable is included, the data always have the option of giving it an estimated coefficient of zero, leaving the predicted values and the ''R''<sup>2</sup> unchanged. The only way that the optimization problem will give a non-zero coefficient is if doing so improves the ''R''<sup>2</sup>. | |||
===Notes on interpreting ''R''<sup>2</sup>=== | |||
''R''² does not indicate whether: | |||
* the independent variables are a cause of the changes in the [[dependent variable]]; | |||
* [[omitted-variable bias]] exists; | |||
* the correct [[regression analysis|regression]] was used; | |||
* the most appropriate set of independent variables has been chosen; | |||
* there is [[Multicollinearity|collinearity]] present in the data on the explanatory variables; | |||
* the model might be improved by using transformed versions of the existing set of independent variables. | |||
==Adjusted ''R''<sup>2</sup>== | |||
{{see also subsection|Omega-squared, ω2|Effect size}} | |||
The use of an adjusted ''R''<sup>2</sup> (often written as <math>\bar R^2</math> and pronounced "R bar squared") is an attempt to take account of the phenomenon of the ''R''<sup>2</sup> automatically and spuriously increasing when extra explanatory variables are added to the model. It is a modification due to Theil<ref>{{cite book | title=Economic Forecasts and Policy | publisher=North | author=Theil, Henri | year=1961 | location=Holland, Amsterdam}}{{Page needed|date=April 2012}}</ref> of ''R''<sup>2</sup> that adjusts for the number of [[explanatory variable|explanatory]] terms in a model relative to the number of data points. The adjusted ''R''<sup>2</sup> can be negative, and its value will always be less than or equal to that of ''R''<sup>2</sup>. Unlike ''R''<sup>2</sup>, the adjusted ''R''<sup>2</sup> increases when a new explanator is included only if the new explanator improves the ''R''<sup>2</sup> more than would be expected in the absence of any explanatory value being added by the new explanator. If a set of explanatory variables with a predetermined hierarchy of importance are introduced into a regression one at a time, with the adjusted ''R''<sup>2</sup> computed each time, the level at which adjusted ''R''<sup>2</sup> reaches a maximum, and decreases afterward, would be the regression with the ideal combination of having the best fit without excess/unnecessary terms. The adjusted ''R''<sup>2</sup> is defined as | |||
:<math>\bar R^2 = {1-(1-R^{2}){n-1 \over n-p-1}} = {R^{2}-(1-R^{2}){p \over n-p-1}}</math> | |||
where ''p'' is the total number of regressors in the linear model (not counting the constant term), and ''n'' is the sample size. | |||
Adjusted ''R''<sup>2</sup> can also be written as | |||
:<math>\bar R^2 = {1-{SS_\text{err}/df_e \over SS_\text{tot}/df_t}}</math> | |||
where ''df''<sub>''t''</sub> is the [[Degrees of freedom (statistics)|degrees of freedom]] ''n''– 1 of the estimate of the population variance of the dependent variable, and ''df''<sub>''e''</sub> is the degrees of freedom ''n'' – ''p'' – 1 of the estimate of the underlying population error variance. | |||
The principle behind the adjusted ''R''<sup>2</sup> statistic can be seen by rewriting the ordinary ''R''<sup>2</sup> as | |||
:<math>R^{2} = {1-{\textit{VAR}_\text{err} \over \textit{VAR}_\text{tot}}}</math> | |||
where <math>{\textit{VAR}_\text{err} = SS_\text{err}/n}</math> and <math>{\textit{VAR}_\text{tot} = SS_\text{tot}/n}</math> are the sample variances of the estimated residuals and the dependent variable respectively, which can be seen as biased estimates of the population variances of the errors and of the dependent variable. These estimates are replaced by statistically [[Bias of an estimator#Sample variance|unbiased]] versions: <math>{\textit{VAR}_\text{err} = SS_\text{err}/(n-p-1)}</math> and <math>{\textit{VAR}_\text{tot} = SS_\text{tot}/(n-1)}</math>. | |||
Adjusted ''R''<sup>2</sup> does not have the same interpretation as ''R''<sup>2</sup>—while ''R''<sup>2</sup> is a measure of fit, adjusted ''R''<sup>2</sup> is instead a comparative measure of suitability of alternative nested sets of explanators. {{citation needed|date=March 2013}} As such, care must be taken in interpreting and reporting this statistic. Adjusted ''R''<sup>2</sup> is particularly useful in the [[feature selection]] stage of model building. | |||
==Generalized ''R''<sup>2</sup>== | |||
Nagelkerke (1991) generalizes the definition of the coefficient of determination: | |||
# A generalized coefficient of determination should be consistent with the classical coefficient of determination when both can be computed; | |||
# Its value should also be maximised by the maximum likelihood estimation of a model; | |||
# It should be, at least asymptotically, independent of the sample size; | |||
# Its interpretation should be the proportion of the variation explained by the model; | |||
# It should be between 0 and 1, with 0 denoting that model does not explain any variation and 1 denoting that it perfectly explains the observed variation; | |||
# It should not have any unit. | |||
The generalized ''R''² (which was itself originally proposed by Cox & Snell (1989) ) has all of these properties. | |||
: <math>R^{2} = 1 - \left({ L(0) \over L(\hat{\theta})}\right)^{2/n}</math> | |||
where ''L''(0) is the likelihood of the model with only the intercept, <math>{L(\hat{\theta})}</math> is the likelihood of the estimated model (i.e., the model with a given set of parameter estimates) and ''n'' is the sample size. | |||
However, in the case of a logistic model, where <math>L(\hat{\theta})</math> cannot be greater than 1, ''R''² is between 0 and <math> R^2_\max = 1- (L(0))^{2/n} </math>: thus, Nagelkerke suggests the possibility to define a scaled ''R''² as ''R''²/''R''²<sub>max</sub>.<ref>{{cite journal |doi=10.1093/biomet/78.3.691 |title=A Note on a General Definition of the Coefficient of Determination |year=1991 |last1=Nagelkerke |first1=N. J. D. |journal=Biometrika |volume=78 |issue=3 |pages=691–2 |jstor=2337038}}</ref> | |||
==Comparison with other goodness of fit indicators== | |||
The higher the correlation, the closer r2 is to "1". | |||
===Norm of Residuals=== | |||
Occasionally the norm of residuals is used for indicating goodness of fit. This term is encountered in [[MATLAB]] and is calculated by | |||
:<math>\text{norm of residuals} = \sqrt{SS_\text{res}} </math> | |||
Both ''R''<sup>2</sup> and the norm of residuals have their relative merits. For [[least squares]] analysis ''R''<sup>2</sup> varies between 0 and 1, with larger numbers indicating better fits and 1 represents a perfect fit. Norm of residuals varies from 0 to infinity with smaller numbers indicating better fits and zero indicating a perfect fit. One advantage and disadvantage of ''R''<sup>2</sup> is the <math>\sqrt{SS_\text{tot}}</math> term acts to [[Normalization (statistics)|normalize]] the value. If the ''y<sub>i</sub>'' values are all multiplied by a constant, the norm of residuals will also change by that constant but ''R''<sup>2</sup> will stay the same. As a basic example, for the linear least squares fit to the set of data: | |||
: <math> | |||
x = 1,\ 2,\ 3,\ 4,\ 5 | |||
</math> | |||
: <math> | |||
y = 1.9,\ 3.7,\ 5.8,\ 8.0,\ 9.6 | |||
</math> | |||
''R''<sup>2</sup> = 0.997, and norm of residuals = 0.302. | |||
If all values of y are multiplied by 1000 (for example, in an [[Metric prefix|SI prefix]] change), then ''R''<sup>2</sup> remains the same, but norm of residuals = 302. | |||
==See also== | |||
* [[Fraction of variance unexplained]] | |||
* [[Goodness of fit]] | |||
* [[Nash–Sutcliffe model efficiency coefficient]] ([[Hydrology|hydrological applications]]) | |||
* [[Pearson product-moment correlation coefficient]] | |||
* [[Proportional reduction in loss]] | |||
* [[Regression model validation]] | |||
* [[Root mean square deviation]] | |||
==Notes== | |||
{{Reflist}} | |||
==References== | |||
{{Refbegin}} | |||
*{{cite book |last=Draper |first=N. R. |last2=Smith |first2=H. |year=1998 |title=Applied Regression Analysis |publisher=Wiley-Interscience |isbn=0-471-17082-8 }} | |||
*{{cite book |last=Everitt |first=B. S. |year=2002 |title=Cambridge Dictionary of Statistics |edition=2nd |publisher=CUP |isbn=0-521-81099-X }} | |||
*{{cite book |last=Nagelkerke |first=Nico J. D. |year=1992 |title=Maximum Likelihood Estimation of Functional Relationships, Pays-Bas |series=Lecture Notes in Statistics |volume=69 |isbn=0-387-97721-X }} | |||
*{{cite book |last=Glantz |first=S. A. |last2=Slinker |first2=B. K. |year=1990 |title=Primer of Applied Regression and Analysis of Variance |publisher=McGraw-Hill |isbn=0-07-023407-8 }} | |||
{{Refend}} | |||
{{DEFAULTSORT:Coefficient Of Determination}} | |||
[[Category:Regression analysis]] | |||
[[Category:Statistical ratios]] | |||
[[Category:Statistical terminology]] | |||
[[Category:Least squares]] | |||
Latest revision as of 01:29, 6 December 2013

In statistics, the coefficient of determination, denoted R2 and pronounced R squared, indicates how well data points fits a statistical model – sometimes simply a line or curve. It is a statistic used in the context of statistical models whose main purpose is either the prediction of future outcomes or the testing of hypotheses, on the basis of other related information. It provides a measure of how well observed outcomes are replicated by the model, as the proportion of total variation of outcomes explained by the model.[1]
There are several different definitions of R2 which are only sometimes equivalent. One class of such cases includes that of simple linear regression. In this case, if an intercept is included then R2 is simply the square of the sample correlation coefficient between the outcomes and their predicted values; in the case of simple linear regression, it is the square of the correlation between the outcomes and the values of the single regressor being used for prediction. If an intercept is included and the number of explanators is more than one, R2 is the square of the coefficient of multiple correlation. In such cases, the coefficient of determination ranges from 0 to 1. Important cases where the computational definition of R2 can yield negative values, depending on the definition used, arise where the predictions which are being compared to the corresponding outcomes have not been derived from a model-fitting procedure using those data, and where linear regression is conducted without including an intercept. Additionally, negative values of R2 may occur when fitting non-linear functions to data.[2] In cases where negative values arise, the mean of the data provides a better fit to the outcomes than do the fitted function values, according to this particular criterion.[3]
Definitions

The better the linear regression (on the right) fits the data in comparison to the simple average (on the left graph), the closer the value of is to one. The areas of the blue squares represent the squared residuals with respect to the linear regression. The areas of the red squares represent the squared residuals with respect to the average value.
A data set has values yi, each of which has an associated modelled value fi (also sometimes referred to as ŷi). Here, the values yi are called the observed values and the modelled values fi are sometimes called the predicted values.
In what follows is the mean of the observed data:
where n is the number of observations.
The "variability" of the data set is measured through different sums of squares:Template:Disambiguation needed
- the total sum of squares (proportional to the sample variance);
- the regression sum of squares, also called the explained sum of squares.
- , the sum of squares of residuals, also called the residual sum of squares.
The notations and should be avoided, since in some texts their meaning is reversed to Residual sum of squares and Explained sum of squares, respectively.
The most general definition of the coefficient of determination is
Relation to unexplained variance
In a general form, R2 can be seen to be related to the unexplained variance, since the second term compares the unexplained variance (variance of the model's errors) with the total variance (of the data). See fraction of variance unexplained.
As explained variance
In some cases the total sum of squares equals the sum of the two other sums of squares defined above,
See partitioning in the general OLS model for a derivation of this result for one case where the relation holds. When this relation does hold, the above definition of R2 is equivalent to
In this form R2 is expressed as the ratio of the explained variance (variance of the model's predictions, which is SSreg / n) to the total variance (sample variance of the dependent variable, which is SStot / n).
This partition of the sum of squares holds for instance when the model values ƒi have been obtained by linear regression. A milder sufficient condition reads as follows: The model has the form
where the qi are arbitrary values that may or may not depend on i or on other free parameters (the common choice qi = xi is just one special case), and the coefficients α and β are obtained by minimizing the residual sum of squares.
This set of conditions is an important one and it has a number of implications for the properties of the fitted residuals and the modelled values. In particular, under these conditions:
As squared correlation coefficient
Similarly, in linear least squares regression with an estimated intercept term, R2 equals the square of the Pearson correlation coefficient between the observed and modeled (predicted) data values of the dependent variable.
Under more general modeling conditions, where the predicted values might be generated from a model different than linear least squares regression, an R2 value can be calculated as the square of the correlation coefficient between the original and modeled data values. In this case, the value is not directly a measure of how good the modeled values are, but rather a measure of how good a predictor might be constructed from the modeled values (by creating a revised predictor of the form α + βƒi). According to Everitt (2002, p. 78), this usage is specifically the definition of the term "coefficient of determination": the square of the correlation between two (general) variables.
Interpretation
R2 is a statistic that will give some information about the goodness of fit of a model. In regression, the R2 coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R2 of 1 indicates that the regression line perfectly fits the data.
Values of R2 outside the range 0 to 1 can occur where it is used to measure the agreement between observed and modeled values and where the "modeled" values are not obtained by linear regression and depending on which formulation of R2 is used. If the first formula above is used, values can be greater than one. If the second expression is used, there are no constraints on the values obtainable.
In many (but not all) instances where R2 is used, the predictors are calculated by ordinary least-squares regression: that is, by minimizing SSerr. In this case R2 increases as we increase the number of variables in the model (R2 is monotone increasing with the number of variables included, i.e. it will never decrease). This illustrates a drawback to one possible use of R2, where one might keep adding variables (Kitchen sink regression) to increase the R2 value. For example, if one is trying to predict the sales of a model of car from the car's gas mileage, price, and engine power, one can include such irrelevant factors as the first letter of the model's name or the height of the lead engineer designing the car because the R2 will never decrease as variables are added and will probably experience an increase due to chance alone.
This leads to the alternative approach of looking at the adjusted R2. The explanation of this statistic is almost the same as R2 but it penalizes the statistic as extra variables are included in the model. For cases other than fitting by ordinary least squares, the R2 statistic can be calculated as above and may still be a useful measure. If fitting is by weighted least squares or generalized least squares, alternative versions of R2 can be calculated appropriate to those statistical frameworks, while the "raw" R2 may still be useful if it is more easily interpreted. Values for R2 can be calculated for any type of predictive model, which need not have a statistical basis.
In a linear model
Consider a linear model of the form
where, for the ith case, is the response variable, are p regressors, and is a mean zero error term. The quantities are unknown coefficients, whose values are estimated by least squares. The coefficient of determination R2 is a measure of the global fit of the model. Specifically, R2 is an element of [0, 1] and represents the proportion of variability in Yi that may be attributed to some linear combination of the regressors (explanatory variables) in X.
R2 is often interpreted as the proportion of response variation "explained" by the regressors in the model. Thus, R2 = 1 indicates that the fitted model explains all variability in , while R2 = 0 indicates no 'linear' relationship (for straight line regression, this means that the straight line model is a constant line (slope = 0, intercept = ) between the response variable and regressors). An interior value such as R2 = 0.7 may be interpreted as follows: "Seventy percent of the variation in the response variable can be explained by the explanatory variables. The remaining thirty percent can be attributed to unknown, lurking variables or inherent variability."
A caution that applies to R2, as to other statistical descriptions of correlation and association is that "correlation does not imply causation." In other words, while correlations may provide valuable clues regarding causal relationships among variables, a high correlation between two variables does not represent adequate evidence that changing one variable has resulted, or may result, from changes of other variables.
In case of a single regressor, fitted by least squares, R2 is the square of the Pearson product-moment correlation coefficient relating the regressor and the response variable. More generally, R2 is the square of the correlation between the constructed predictor and the response variable. With more than one regressor, the R2 can be referred to as the coefficient of multiple determination.
Inflation of R2
In least squares regression, R2 is weakly increasing with increases in the number of regressors in the model. Because increases in the number of regressors increase the value of R2, R2 alone cannot be used as a meaningful comparison of models with very different numbers of independent variables. For a meaningful comparison between two models, an F-test can be performed on the residual sum of squares, similar to the F-tests in Granger causality, though this is not always appropriate. As a reminder of this, some authors denote R2 by Rp2, where p is the number of columns in X (the number of explanators including the constant).
To demonstrate this property, first recall that the objective of least squares linear regression is:
The optimal value of the objective is weakly smaller as additional columns of are added, by the fact that less constrained minimization leads to an optimal cost which is weakly smaller than more constrained minimization does. Given the previous conclusion and noting that depends only on y, the non-decreasing property of R2 follows directly from the definition above.
The intuitive reason that using an additional explanatory variable cannot lower the R2 is this: Minimizing is equivalent to maximizing R2. When the extra variable is included, the data always have the option of giving it an estimated coefficient of zero, leaving the predicted values and the R2 unchanged. The only way that the optimization problem will give a non-zero coefficient is if doing so improves the R2.
Notes on interpreting R2
R² does not indicate whether:
- the independent variables are a cause of the changes in the dependent variable;
- omitted-variable bias exists;
- the correct regression was used;
- the most appropriate set of independent variables has been chosen;
- there is collinearity present in the data on the explanatory variables;
- the model might be improved by using transformed versions of the existing set of independent variables.
Adjusted R2
First, the rate for a bad credit loan is greater than a conventional home loan. You may come across many people who have been chucked out of their jobs. Closing a card with balance due on it might give you blemished credit if the lender stops reporting your borrowing limit. If, on the other hand, your account is still in the statute but the account has been re-aged, you will also need documented proof of the evidence and bring it to court. So it's very important that you know more about the types of cards available, and one that will work best for you.
You must always search around to get the best deal with your home loan. Thousands of online searches are actually inquired every week regarding poor credit credit charge cards as well as personal loan concerns. State governments can encourage developers to build in larger quantities at reasonable sizes and affordable prices in a public-private partnership approach. Some firms could give cost-free credit constructing and following that possess a hidden charge, this may possibly simultaneously be a scam. You'll opt for either secured or unsecured poor credit personal loans relying upon your wants.
And, then you start running in the opposite direction and run as fast as you can. Most times, students get credit from finance institution through this implies. To avoid perpetuating their monetary crises, borrowers should not take out these kinds of loan unless it's urgent, and they should always consider a payment schedule beforehand. Having a poor credit ranking may limit you heavily in both situations. In deed so, you tins become familiar with different terms of importance postcard and rates.
It is no longer difficult to borrow money despite poor credit. Poor credit people can improve their credit rating by repaying the loan amount regularly and in time. Poor credit loans are the sort of advances which will never include any sort of credit check policy or so on. But this time it is really important to choose the right offer for you, because few bad decisions can make you go through hard times for instance borrowing more than you can afford, borrowing money for things that can be avoided. If the circumstance is in fact that the report is correct, you are able to have it revised.
Too often, dealers cherry pick these buyers- they pull credits and if the shoppers rating doesn't meet the dealers criterion, the buyer is given the heave-ho. The happy news is that when you are putting down payment of ten % or even more than this, the payment of interest will be less. If you liked this short article and you would certainly such as to receive even more info pertaining to egtrend.com; Learn Even more Here, kindly visit our own web page. Here the borrowers can compare the loan deals offered by various lenders. This happens because money lenders approve such loans without conducting any credit checks. In this online guide, we will review the benefits and drawbacks of a 2nd chance unsecured credit card for someone having a damaged credit score.
The use of an adjusted R2 (often written as and pronounced "R bar squared") is an attempt to take account of the phenomenon of the R2 automatically and spuriously increasing when extra explanatory variables are added to the model. It is a modification due to Theil[4] of R2 that adjusts for the number of explanatory terms in a model relative to the number of data points. The adjusted R2 can be negative, and its value will always be less than or equal to that of R2. Unlike R2, the adjusted R2 increases when a new explanator is included only if the new explanator improves the R2 more than would be expected in the absence of any explanatory value being added by the new explanator. If a set of explanatory variables with a predetermined hierarchy of importance are introduced into a regression one at a time, with the adjusted R2 computed each time, the level at which adjusted R2 reaches a maximum, and decreases afterward, would be the regression with the ideal combination of having the best fit without excess/unnecessary terms. The adjusted R2 is defined as
where p is the total number of regressors in the linear model (not counting the constant term), and n is the sample size.
Adjusted R2 can also be written as
where dft is the degrees of freedom n– 1 of the estimate of the population variance of the dependent variable, and dfe is the degrees of freedom n – p – 1 of the estimate of the underlying population error variance.
The principle behind the adjusted R2 statistic can be seen by rewriting the ordinary R2 as
where and are the sample variances of the estimated residuals and the dependent variable respectively, which can be seen as biased estimates of the population variances of the errors and of the dependent variable. These estimates are replaced by statistically unbiased versions: and .
Adjusted R2 does not have the same interpretation as R2—while R2 is a measure of fit, adjusted R2 is instead a comparative measure of suitability of alternative nested sets of explanators. Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park. As such, care must be taken in interpreting and reporting this statistic. Adjusted R2 is particularly useful in the feature selection stage of model building.
Generalized R2
Nagelkerke (1991) generalizes the definition of the coefficient of determination:
- A generalized coefficient of determination should be consistent with the classical coefficient of determination when both can be computed;
- Its value should also be maximised by the maximum likelihood estimation of a model;
- It should be, at least asymptotically, independent of the sample size;
- Its interpretation should be the proportion of the variation explained by the model;
- It should be between 0 and 1, with 0 denoting that model does not explain any variation and 1 denoting that it perfectly explains the observed variation;
- It should not have any unit.
The generalized R² (which was itself originally proposed by Cox & Snell (1989) ) has all of these properties.
where L(0) is the likelihood of the model with only the intercept, is the likelihood of the estimated model (i.e., the model with a given set of parameter estimates) and n is the sample size.
However, in the case of a logistic model, where cannot be greater than 1, R² is between 0 and : thus, Nagelkerke suggests the possibility to define a scaled R² as R²/R²max.[5]
Comparison with other goodness of fit indicators
The higher the correlation, the closer r2 is to "1".
Norm of Residuals
Occasionally the norm of residuals is used for indicating goodness of fit. This term is encountered in MATLAB and is calculated by
Both R2 and the norm of residuals have their relative merits. For least squares analysis R2 varies between 0 and 1, with larger numbers indicating better fits and 1 represents a perfect fit. Norm of residuals varies from 0 to infinity with smaller numbers indicating better fits and zero indicating a perfect fit. One advantage and disadvantage of R2 is the term acts to normalize the value. If the yi values are all multiplied by a constant, the norm of residuals will also change by that constant but R2 will stay the same. As a basic example, for the linear least squares fit to the set of data:
R2 = 0.997, and norm of residuals = 0.302. If all values of y are multiplied by 1000 (for example, in an SI prefix change), then R2 remains the same, but norm of residuals = 302.
See also
- Fraction of variance unexplained
- Goodness of fit
- Nash–Sutcliffe model efficiency coefficient (hydrological applications)
- Pearson product-moment correlation coefficient
- Proportional reduction in loss
- Regression model validation
- Root mean square deviation
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
- ↑ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, pp. 187, 287.)
- ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ Template:Cite web
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534Template:Page needed - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang