Néel relaxation theory: Difference between revisions
en>Bibcode Bot m Adding 0 arxiv eprint(s), 1 bibcode(s) and 0 doi(s). Did it miss something? Report bugs, errors, and suggestions at User talk:Bibcode Bot |
en>RockMagnetist m formatting |
||
| Line 1: | Line 1: | ||
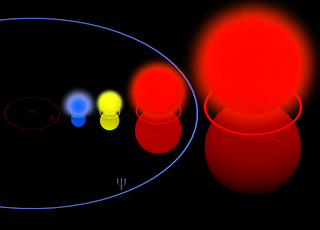
[[Image:Rho Cassiopeiae Sol VY Canis Majoris.png|320px|center|Some massive stars compared to our Sun ( one single grey pixel in the 'Full resolution' image (2,876 × 2,068 pixels)) and the orbit of Earth (grey), Jupiter (red) and Neptune (blue). From left to right: The Pistol Star, Rho Cassiopeiae, Betelgeuse, and VY Canis Majoris]] | |||
<center><small>Photo credit: [[commons:User:Anynobody|user:Anynobody]]</small></center> | |||
The '''[[solar mass]]''' (<math>\begin{smallmatrix}M_\odot\end{smallmatrix}</math>) is a standard [[units of mass|unit of mass]] in [[astronomy]], used to indicate the masses of other [[star]]s, as well as [[Star cluster|cluster]]s, [[nebula]]e and [[galaxy|galaxies]]. It is equal to the mass of the [[Sun]], about two [[Names of large numbers|nonillion]] [[kilogram]]s. This is about 332,950 times the mass of the [[Earth]] or 1,048 times the mass of [[Jupiter]]. Because the Earth follows an [[elliptical orbit]] around the Sun, the solar mass can be computed from the equation for the [[orbital period]] of a small body orbiting a central mass. Based upon the length of the year, the distance from the Earth to the Sun (an [[astronomical unit]] or AU), and the [[gravitational constant]] (''G''). | |||
The value of the gravitational constant was derived from 1798 measurements by [[Henry Cavendish]] using a [[torsion balance]]. The value obtained differed only by about 1% from the modern value.The [[parallax#Diurnal parallax|diurnal parallax]] of the [[Sun]] was accurately measured during the transits of Venus in 1761 and 1769, yielding a value of 9″ (compared to the present 1976 value of 8.794148″), yielding a value of 9″ (compared to the present 1976 value of 8.794148″). When the value of the diurnal parallax is known, the distance to the Sun can be determined from the geometry of the Earth. | |||
The first person to estimate the mass of the Sun was [[Isaac Newton]]. In his work ''[[Principia]]'', he estimated that the ratio of the mass of the Earth to the Sun was about 1/28,700. Later he determined that this value was based upon a faulty value for the solar parallax, which was used to estimate the distance to the Sun (1 AU). He revised his result to obtain a ratio of 1/169,282 in the third edition of the ''Principia''. The current value for the solar parallax is smaller still, giving a mass ratio of 1/332,946. | |||
As a unit of measurement, the solar mass came into use before the AU and the gravitational constant were precisely measured. This is because the determination of the relative mass of another planet in the [[Solar System]] or of a [[Binary star#Use in astrophysics|binary star]] in units of solar masses does not depend on these poorly known constants. So it was useful to express these masses in units of solar masses (see [[Gaussian gravitational constant]]). | |||
The mass of the Sun changes slowly, compared to the lifetime of the Sun. Mass is lost due to two main processes in nearly equal amounts. First, in the [[Solar core|Sun's core]] hydrogen is converted into helium by [[nuclear fusion]], in particular the [[Proton–proton chain reaction|pp chain]]. Thereby mass is converted to energy in correspondence to the [[mass–energy equivalence]]. This energy is eventually [[Solar luminosity|radiated away]] by the Sun. The second process is the [[solar wind]], which is the ejection of mainly protons and electrons to outer space. The actual net mass of the Sun since it reached the [[main sequence]] remains uncertain. The early Sun had much higher mass loss rates than at present, so, realistically, it may have lost anywhere from 1–7% of its total mass over the course of its main sequence lifetime. | |||
'''<center>[[Solar mass|Read more...]]</center>''' | |||
Latest revision as of 06:53, 26 October 2013
The solar mass () is a standard unit of mass in astronomy, used to indicate the masses of other stars, as well as clusters, nebulae and galaxies. It is equal to the mass of the Sun, about two nonillion kilograms. This is about 332,950 times the mass of the Earth or 1,048 times the mass of Jupiter. Because the Earth follows an elliptical orbit around the Sun, the solar mass can be computed from the equation for the orbital period of a small body orbiting a central mass. Based upon the length of the year, the distance from the Earth to the Sun (an astronomical unit or AU), and the gravitational constant (G).
The value of the gravitational constant was derived from 1798 measurements by Henry Cavendish using a torsion balance. The value obtained differed only by about 1% from the modern value.The diurnal parallax of the Sun was accurately measured during the transits of Venus in 1761 and 1769, yielding a value of 9″ (compared to the present 1976 value of 8.794148″), yielding a value of 9″ (compared to the present 1976 value of 8.794148″). When the value of the diurnal parallax is known, the distance to the Sun can be determined from the geometry of the Earth. The first person to estimate the mass of the Sun was Isaac Newton. In his work Principia, he estimated that the ratio of the mass of the Earth to the Sun was about 1/28,700. Later he determined that this value was based upon a faulty value for the solar parallax, which was used to estimate the distance to the Sun (1 AU). He revised his result to obtain a ratio of 1/169,282 in the third edition of the Principia. The current value for the solar parallax is smaller still, giving a mass ratio of 1/332,946.
As a unit of measurement, the solar mass came into use before the AU and the gravitational constant were precisely measured. This is because the determination of the relative mass of another planet in the Solar System or of a binary star in units of solar masses does not depend on these poorly known constants. So it was useful to express these masses in units of solar masses (see Gaussian gravitational constant).
The mass of the Sun changes slowly, compared to the lifetime of the Sun. Mass is lost due to two main processes in nearly equal amounts. First, in the Sun's core hydrogen is converted into helium by nuclear fusion, in particular the pp chain. Thereby mass is converted to energy in correspondence to the mass–energy equivalence. This energy is eventually radiated away by the Sun. The second process is the solar wind, which is the ejection of mainly protons and electrons to outer space. The actual net mass of the Sun since it reached the main sequence remains uncertain. The early Sun had much higher mass loss rates than at present, so, realistically, it may have lost anywhere from 1–7% of its total mass over the course of its main sequence lifetime.