Hilbert scheme: Difference between revisions
| Line 1: | Line 1: | ||
[[Image:HyperbolicParaboloid.png|thumb|right|[[Hyperbolic paraboloid]]]] | |||
[[Image:Ruled hyperboloid.jpg|thumb|right|A model of an [[elliptic hyperboloid]] of one sheet]] | |||
[[Image:Monkey Saddle Surface (Shaded).png|thumb|right|A [[monkey saddle]]|300px]] | |||
A '''saddle surface''' is a [[smooth surface]] containing one or more [[saddle point]]s. The term derives from the peculiar shape of historical<!--modern [[saddle]]s evolved away from clean-cut "saddle surface"--> [[horse]] [[saddle]]s, which curve both up and down. | |||
Classical examples of two-dimensional saddle surfaces in the [[Euclidean space]] are second order surfaces, the [[hyperbolic paraboloid]] <math>z=x^2-y^2</math> (which is often referred to as '''the''' saddle surface or "the standard saddle surface") and the [[hyperboloid of one sheet]]. The [[Pringles]] potato chip or crisp is an everyday example of a hyperbolic paraboloid shape. | |||
Saddle surfaces have negative [[Gaussian curvature]] which distinguish them from convex/elliptical surfaces which have positive Gaussian curvature. A classical third-order saddle surface is the [[monkey saddle]]. | |||
The Ph.D. thesis of [[Grigori Perelman]], titled "Saddle surfaces in Euclidean spaces," was devoted to saddle surfaces.<ref>{{cite book|author=Перельман, Григорий Яковлевич |title=Седловые поверхности в евклидовых пространствах: Автореф. дис. на соиск. учен. степ. канд. физ.-мат. наук|language=Russian| publisher=Ленинградский Государственный Университет| year=1990}}</ref> | |||
== References == | |||
* {{cite book | |||
| author = [[David Hilbert|Hilbert, David]]; Cohn-Vossen, Stephan | |||
| title = Geometry and the Imagination | |||
| edition = 2nd | |||
| year = 1952 | |||
| publisher = Chelsea | |||
| isbn = 0-8284-1087-9}} | |||
{{reflist}} | |||
{{DEFAULTSORT:Saddle Surface}} | |||
[[Category:Multivariable calculus]] | |||
[[Category:Surfaces]] | |||
Latest revision as of 04:45, 23 November 2013
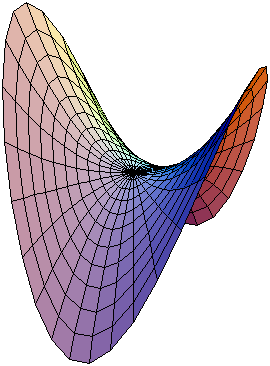


A saddle surface is a smooth surface containing one or more saddle points. The term derives from the peculiar shape of historical horse saddles, which curve both up and down.
Classical examples of two-dimensional saddle surfaces in the Euclidean space are second order surfaces, the hyperbolic paraboloid (which is often referred to as the saddle surface or "the standard saddle surface") and the hyperboloid of one sheet. The Pringles potato chip or crisp is an everyday example of a hyperbolic paraboloid shape.
Saddle surfaces have negative Gaussian curvature which distinguish them from convex/elliptical surfaces which have positive Gaussian curvature. A classical third-order saddle surface is the monkey saddle.
The Ph.D. thesis of Grigori Perelman, titled "Saddle surfaces in Euclidean spaces," was devoted to saddle surfaces.[1]
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534